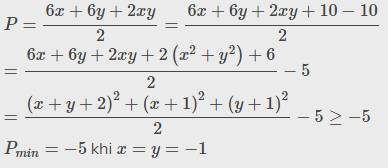Các câu hỏi tương tự
Cho các số thực x và y thoả mãn điều kiện x^2+y^2=2. tìm giá trị nhỏ nhất của biểu thức P=3(x+y)+xy
cho các số thực x và y thỏa mãn điều kiện x^2 + y^2 = 2 Tìm giá trị nhỏ nhất của biểu thức P = 3(x+y)+xy
Cho các số thực dương x,y thoả mãn: (x+y-1)^2= xy . Tìm giá trị nhỏ nhất của biểu thức P=1/xy + 1/x^2+y^2 + căn(xy)/x+y
\(\text{Các số thực không âm x,y,z thay đổi thỏa mãn điều kiện: x^2+ y^2+x^2+x^2y^2+y^2z^2+z^2x^2=6. \text{Tìm giá trị lớn nhất và nhỏ nhất của biểu thức Q=x+y+z}}\)\(\text{Các số thực không âm x,y,z thay đổi thỏa mãn điều kiện x^2+y^2+z^2+x^2y^2+y^2z^2+z^2x^2=6. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức Q=x+y+z}\)
Gọi x, y là các số thực thay đổi , thỏa mãn điều kiện: x>y>0 và xy=4
Tìm giá trị nhỏ nhất của biểu thức: \(P=\frac{x^2+y^2}{x-y+1}\)
cho các số thực dương x,y thỏa mãn điều kiện x+y=2016.Tìm giá trị nhỏ nhất của biểu thức:
P=\(\sqrt{5x^2+xy+3y^2}+\sqrt{3x^2+xy+5y^2}+\sqrt{x^2+xy+2y^2}+\sqrt{2x^2+xy+y^2}\)
Cho x,y là các số thỏa mãn điều kiện x+y = 1. Tìm giá trị nhỏ nhất của biểu thức C = \(x^2+y^2+xy\)
Cho các số thực x,y thoả mãn x+y 2.Tìm giá trị nhỏ nhất của biểu thức: A x3�3 + y3�3 + x2�2 + y2
Đọc tiếp
Cho các số thực x,y thoả mãn x+y =2.Tìm giá trị nhỏ nhất của biểu thức: A= + + +
giả sử x, y là các số thực dương thoả mãn điều kiện \(\left(\sqrt{x}+1\right)\left(\sqrt{y}+1\right)\ge4\). tìm giá trị nhỏ nhất của biểu thức \(P=\frac{x^2}{y}+\frac{y^2}{x}\)