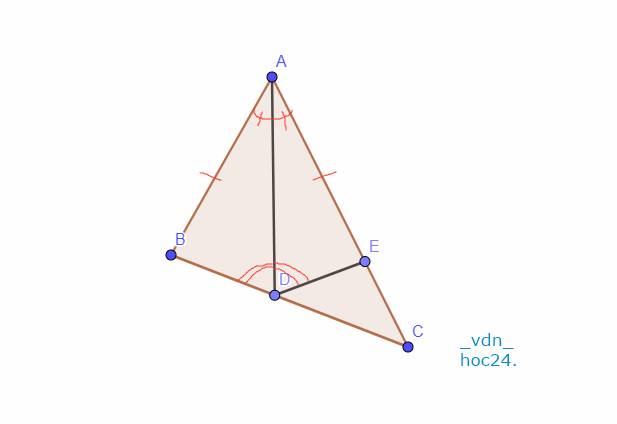
Cho hình vẽ . Chứng minh
a)▲ACE=▲ABE
b) AE là tia phân giác góc BAC
a/ Xét tam giác ABC có: AB = AC (gt) => Tam giác ABC cân tại A
Xét tam giác ABE và tam giác ACE:
^B = ^C (tam giác ABC cân tại A)
^BAE = ^CAE (AE là tia phân giác của góc BAC)
AB = AC (tam giác ABC cân tại A)
=> Tam giác ABE = Tam giác ACE (g c g)
b/ Xét tam giác ABC cân tại A: AE là tia phân giác của góc BAC (gt)
=> AE là đường trung trực của đoạn thẳng BC (TC các đường trong tam giác cân)
Cho tam giác ABC cân. Trên tia đối BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE
a) Góc ABD = góc ACE
b) Góc DAB = góc CAE
c) Vẽ BH vuông góc với AD ( H thuộc AD ), vẽ CK vuông góc với AE ( K thuộc AE ). Chứng minh BH = CK; góc HBD = góc kcs
d) Tia HB cắt KC tại I. Chứng minh AI là phân giác của góc BAC
Cho tam giác ABC; AB=AC. Trên tia đối của tia BC lấy điểm D; và trên tua đối của tia CB lấy điểm E sao cho BD=CE. KẺ BH vuông góc AD( H thuộc AD); CK vuông góc AE( K thuộc AE).
a, Chứng minh: Tam giác ABD= Tam giác ACE; tam giác ACD= tam giác ABE
b, Chứng minh: BH=CK
c, Gọi M, N tương ứng là trung điểm của HK,BC; và I=BH Ω CK. Chứng minh rằng: A,M,N,I thẳng hàng.
GIÚP MINH VỚI MÌNH ĐANG THI NÊN CẦN GẤP LẮM. CHO MÌNH CẢ HÌNH VẼ NỮA NHÉ.
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔACD và ΔABE có
AC=AB
CD=BE
AD=AE
Do đó: ΔACD=ΔABE
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
Suy ra: BH=CK
Cho mình xin hình vẽ với câu c nữa. Mình cảm ơn nhiều lắm huhuhhhu
Cho tam giác ABC có AD là đường phân giác. Vẽ tia CE sao cho góc ACE và góc BAC so le trong. Vẽ tia CM là tia phân giác của góc ACE. Chứng minh rằng:
a, AB//CE
b,AD//CM
Bài này có sẵn đk hểt rồi mà
a/ ta có góc BAC= góc ACE (gt)
mà 2 góc so le trong chỉ bằng khi hai cạnh tạo ra hai góc đó song song
=> AB//CE
b/ ta có góc BAC=góc ACE
mà góc DAC=1/2 góc BAC
góc AMC=1/2 góc ACE
=> góc DAC=góc ACM
mà 2 góc này nằm ở vị trí so le trong
=> AD//CM
tick cho mình nha bạn
Cho tam giác ABC có AD là đường phân giác. Vẽ tia CE sao cho góc ACE và góc BAC so le trong. Vẽ tia CM là tia phân giác của góc ACE. Chứng minh rằng:
a) AB// CE
b) AD// CM
a,Vì ACE và BAC là hai góc so le trong =>AB // CE ( tính chất hai đường thẳng song song)
b,Vì AD là phân giác của BAC=>BAD=DAC
Vì CM là phân giác của ACE=>ACM=MCE
Ta có : ACE=BAC(hai góc so le trong)
=> 1/2 ACE= 1/2 BAC
hay DAC=ACM
Mà hai góc này nằm ở vị trí so le trong => AD//CM
Cho tam giác ABC vuông ở C, có góc A bằng 60, tia phân giác của góc BAC cắt BC tại E. Kẻ EK vuông góc với AB tại K. a. Chứng minh: ACE = AKE b. Kẻ BD vuông góc với AE tại D. Chứng minh: AD = BC
a: Xét ΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
góc CAE=góc KAE
=>ΔACE=ΔAKE
b: Xét ΔEAB có góc EAB=góc EBA
nên ΔEAB cân tại E
=>EA=EB
Xét ΔECA vuông tại C và ΔEDB vuông tại D có
EA=EB
góc AEC=góc BED
=>ΔECA=ΔEDB
=>EC=ED
=>AD=BC
Cho tam giác ABC vuông ở C có góc A=60*vẽ AE là phân giác cuar góc BAC(E thuộc BC). K ẻ BD vuông góc với tia AE (D thộc AE)
a) Chứng minh tam giác ABD cân
b) Chứng minh tam giác ABD bằng tam giác BAC
c) AC cắt BD tại I . Chứng minh K , E , I thẳng hàng
Cho tam giác ABC có AB < AC . Phân giác của góc A cắt cạnh BC tại điểm D. Trên cạnh AC lấy điểm E sao cho AE = AB. Chứng minh
a) ∆ A B D = ∆ A E D .
b) DA là tia phân giác của góc BDE. Từ đó suy ra A B C ^ > A C B ^ .
\(\text{#TNam}\)
`a,` \(\text{Xét Tam giác ABD và Tam giác AED có:}\)
`AB = AE (g``t)`
\(\widehat{BAD}=\widehat{EAD} (\text {tia phân giác} \) \(\widehat{BAE})\)
`\text {AD chung}`
`=> \text {Tam giác ABD = Tam giác AED (c-g-c)}`
`b,`
\(\text{Vì Tam giác ABD = Tam giác AED (a)}\)
`->`\(\widehat{ADB}=\widehat{ADE} (\text {2 góc tương ứng})\)
`-> \text {AD là tia phân giác}` \(\widehat{BDE}\)
\(\text{Xét Tam giác ABC:}\)
`AC > AB (g``t)`
\(\text{Theo định lý của quan hệ giữa góc và cạnh đối diện trong 1 tam giác}\)
`->`\(\widehat{ABC}>\widehat{ACB}.\)
bài 3: Cho tam giác ABC vuông ở C, có góc A bằng 60 độ. Tia phân giác của góc BAC cắt BC ở E. Kẻ EK vuông góc với AB (K thuộc AB). Kẻ BD vuông góc với tia AE (D thuộc AE). Chứng minh:
a) AC=AK
b) AE là đường trung trực của CK
Các bạn vẽ hình ghi giả thiết, kết luận luôn nha bài này ghi giả thiết kết luận khó quá mình không biết làm nên các bạn giải dùm mình với mình cảm ơn các bạn
a: XétΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
\(\widehat{CAE}=\widehat{KAE}\)
Do đó; ΔACE=ΔAKE
Suy ra: AC=AK
b: Ta có: ΔACE=ΔAKE
nên EC=EK
mà AC=AK
nên AE là đường trung trực của CK
Cho tam giác ABC có AB=AC, M là trung điểm của AB.M là trung điểm AB,AE là tia phân giác góc BAC (E thuộc BC).Trên tia đối của tia MC lấy điểm K sao cho MC=MK
a. Chứng minh rằng: BK//AC
b. Chứng minh tam giác ACE=tam giác ABE
c. đường thẳng KB cắt AE ở I.CM tam giác IAK vuông
a: Xét tứ giác AKBC có
M là trung điểm của đường chéo CK
M là trung điểm của đường chéo AB
Do đó: AKBC là hình bình hành
Suy ra: BK//AC
b: Xét ΔABE và ΔACE có
AB=AC
\(\widehat{BAE}=\widehat{CAEE}\)
AE chung
Do đó: ΔABE=ΔACE