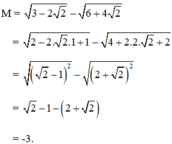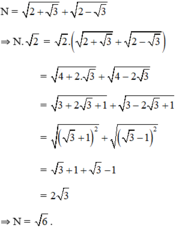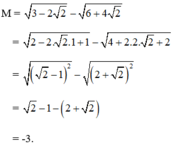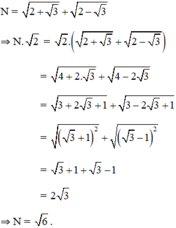42n :16n-1=642011

Những câu hỏi liên quan
l i m 4 n 2 + 5 - n + 4 2 n - 1 bằng:
A. 0
B. 1
C. 2
D. +∞
- Cách 1: Chia tử thức và mẫu thức cho n:
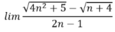
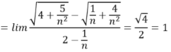
Đáp án là B
- Cách 2: Thực chất có thể coi bậc cao nhất của tử thức và mẫu thức là 1, do đó chỉ cần để ý hệ số bậc 1 của tử thức là √4, của mẫu thức là 2, từ đó tính được kết quả bằng 1. Đáp án B
Đúng 0
Bình luận (0)
a) Với giá trị nào của n thì 4 2 n là phân số?
b) Tìm số nguyên n sao cho phân số 4 2n − 3 có giá trị là số nguyên.
Cho n ∈ N. Chứng minh rằng:
a) 5n+2 + 26.5n + 82n+1 ⋮ 59.
b) ( 42n - 32n - 7 ) ⋮ 168 ( n ≥ 1 ).
a) \(5^{n+2}+26.5^n+8^{2n+1}=25.5^n+26.6^n+8.8^{2n}\)
\(=5^n.51+8.64^n\)
Có \(64\equiv5\) (mod 59)
\(\Rightarrow64^n\equiv5^n\) (mod 59)
\(\Rightarrow8.64^n\equiv8.5^n\) (mod 59)
\(\Rightarrow5^n.51+8.64^n\equiv8.5^n+5^n.51\) (mod 59)
mà \(8.5^n+5^n.51=59.5^n\)\(\equiv0\) (mod 59)
\(\Rightarrow5^n.51+8.64^n\equiv8.5^n+5^n.51\equiv0\) (mod 59)
\(\Rightarrow5^{n+2}+26.5^n+8^{2n+1}⋮59\)
b) \(4^{2n}-3^{2n}-7=16^n-9^n-7\)
Có \(16^n-9^n-7=\left(16-9\right)\left(16^{n-1}+...+9^{n-1}\right)-7=7\left(16^{n-1}+...+9^{n-1}\right)-7⋮\)\(7\) (I)
Có \(16\equiv1\) (mod 3) \(\Rightarrow16^n\equiv1\) (mod 3) mà \(7\equiv1\) (mod 3)
\(\Rightarrow16^n-7\equiv0\) (mod 3) mà \(9^n\equiv0\) (mod 3)
\(\Rightarrow16^n-9^n-7⋮3\) (II)
Có \(9^n\equiv1\) (mod 8)\(\Rightarrow9^n+7\equiv8\) (mod 8)
\(\Rightarrow9^n+7⋮8\) mà \(16^n=2^n.8^n⋮8\)
\(\Rightarrow16^n-9^n-7⋮8\) (III)
Do \(\left(3;7;8\right)=1\)\(,3.7.8=168\)
Từ (I) (II) (III) \(\Rightarrow16^n-9^n-7⋮168\)
\(\Rightarrow\) Đpcm
Đúng 1
Bình luận (0)
a) 5n+2+26.5n+82n+1=25.5n+26.6n+8.82n5n+2+26.5n+82n+1=25.5n+26.6n+8.82n
=5n.51+8.64n=5n.51+8.64n
Có 64≡564≡5 (mod 59)
⇒64n≡5n⇒64n≡5n (mod 59)
⇒8.64n≡8.5n⇒8.64n≡8.5n (mod 59)
⇒5n.51+8.64n≡8.5n+5n.51⇒5n.51+8.64n≡8.5n+5n.51 (mod 59)
mà 8.5n+5n.51=59.5n8.5n+5n.51=59.5n≡0≡0 (mod 59)
⇒5n.51+8.64n≡8.5n+5n.51≡0⇒5n.51+8.64n≡8.5n+5n.51≡0 (mod 59)
Đúng 1
Bình luận (1)
cho e hỏi là 3 dấu gạch ngang là gì vậy ạ
Cho n là số tự nhiên chẵn. CMR: A=20n+16n−3n−1A=20n+16n−3n−1 chia hết cho 323
Nhận thấy 323=17.19323=17.19 và (17;19)=1(17;19)=1 nên ta cần chứng minh 20n−1+16n−3n20n−1+16n−3n chia hết cho số 1717 và 1919
Ta có
20n−1⋮(20−1)=19;16n−3n⋮(16+3)=1920n−1⋮(20−1)=19;16n−3n⋮(16+3)=19 (vì nn chẵn) (∗)(∗)
Mặt khác
20n+16n−3n−1=20n−3n+16n−120n+16n−3n−1=20n−3n+16n−1
và 20n−3n⋮(20−3)=17;16n−1⋮(16+1)=1720n−3n⋮(20−3)=17;16n−1⋮(16+1)=17 (∗∗)(∗∗)
Từ (∗)(∗∗)(∗)(∗∗) ta suy ra đpcm
Đúng 0
Bình luận (0)
Nhận thấy 323=17.19323=17.19 và (17;19)=1(17;19)=1 nên ta cần chứng minh 20n−1+16n−3n20n−1+16n−3n chia hết cho số 1717 và 1919
Ta có
20n−1⋮(20−1)=19;16n−3n⋮(16+3)=1920n−1⋮(20−1)=19;16n−3n⋮(16+3)=19 (vì nn chẵn) (∗)(∗)
Mặt khác
20n+16n−3n−1=20n−3n+16n−120n+16n−3n−1=20n−3n+16n−1
và 20n−3n⋮(20−3)=17;16n−1⋮(16+1)=1720n−3n⋮(20−3)=17;16n−1⋮(16+1)=17 (∗∗)(∗∗)
Từ (∗)(∗∗)(∗)(∗∗) ta suy ra đpcm
Đúng 0
Bình luận (0)
Nhận thấy 323=17.19323=17.19 và (17;19)=1(17;19)=1 nên ta cần chứng minh 20n−1+16n−3n20n−1+16n−3n chia hết cho số 1717 và 1919
Ta có
20n−1⋮(20−1)=19;16n−3n⋮(16+3)=1920n−1⋮(20−1)=19;16n−3n⋮(16+3)=19 (vì nn chẵn) (∗)(∗)
Mặt khác
20n+16n−3n−1=20n−3n+16n−120n+16n−3n−1=20n−3n+16n−1
và 20n−3n⋮(20−3)=17;16n−1⋮(16+1)=1720n−3n⋮(20−3)=17;16n−1⋮(16+1)=17 (∗∗)(∗∗)
Từ (∗)(∗∗)(∗)(∗∗) ta suy ra đpcm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
l i m 4 n 2 + 5 + n + 4 2 n - 3 bằng:
A. 0
B. 1
C. 2
D. +∞
Chọn B
lim 4 n 2 + 5 + n + 4 2 n − 3 = lim 4 + 5 n 2 + 1 n + 4 n 2 2 − 3 n = 1
Đúng 0
Bình luận (0)
Tính giới hạn
T
l
i
m
16
n
+
1
+
4
n
-...
Đọc tiếp
Tính giới hạn T = l i m 16 n + 1 + 4 n - 16 n + 1 + 3 n
A. T = 0
B. T = 1 4
C. T = 1 8
D. T = 1 16
tìm n để 36n+6/42n+14 có thể rút gọn
Ta có 36n+6/42n+14=18n+3/21n+7
Gọi d là ước nguyên tố chung của 18n+3 và 21n+7
Suy ra 18n+3 chia hết cho d, 21n+7 chia hết cho d
Suy ra 7.(18n+3)=126n+21 chia hết cho d, 6.(21n+7) chia hết cho d
Suy ra 126n+21 chia hết cho d, 126+42 chia hết cho d
Ta có
(126n+42)-(126n+21)=126n+42-126n-21=21 chia hết cho d
Mà d nguyên tố nên d thuộc {3;7}
Với d=3 thì 18n+3 chia hết cho 3, luôn đúng
21n+7 chia hết cho 3, vô lí ( loại)
Với d=7 thì 18n+3 chia hết cho 7 suy ra 18n+3-21 chia hết cho 7 hay 18n-18 chia hết cho 7
Suy ra 18.(n-1) chia hết cho 7. Mà (18,7)=1 nên n-1 chia hết cho 7 suy ra n=7k+1 (k thuộc Z)
21n+7 chia hết cho 7, luôn đúng
Vậy với n=7k+1(k thuộc Z) thì phân số rút gọn được
Đúng 0
Bình luận (0)
Rút gọn các biểu thức:
M
3
−
2
2
−
6
+
4
2
N
2
+
3...
Đọc tiếp
Rút gọn các biểu thức:
M = 3 − 2 2 − 6 + 4 2 N = 2 + 3 + 2 − 3
Rút gọn các biểu thức:
M
3
−
2
2
−
6
+
4
2
N
2
+
3...
Đọc tiếp
Rút gọn các biểu thức:
M = 3 − 2 2 − 6 + 4 2 N = 2 + 3 + 2 − 3
Tìm n biết 16n+7n chia hết cho n+1