a: Xét (O) có

ΔBAC nội tiếp

BC là đường kính

Do đó: ΔBAC vuông tại A

=>\(\widehat{ACB}=30^0\)

\(\Leftrightarrow\widehat{ABC}=60^0\)

b: \(AC=6\sqrt{3}\left(cm\right)\)

\(C=AB+AC+BC=6+12+6\sqrt{3}=18+6\sqrt{3}\left(cm\right)\)

\(S=\dfrac{6\sqrt{3}\cdot6}{2}=18\sqrt{3}\left(cm^2\right)\)

c: Xét (O) có

MA là tiếp tuyến

MC là tiếp tuyến

Do đó: MA=MC

hay M nằm trên đường trung trực của AC(1)

Ta có: OA=OC

nên O nằm trên đường trung trực của AC(2)

Từ (1) và (2) suy ra OM là đường trung trực của AC

hay OM\(\perp\)AC

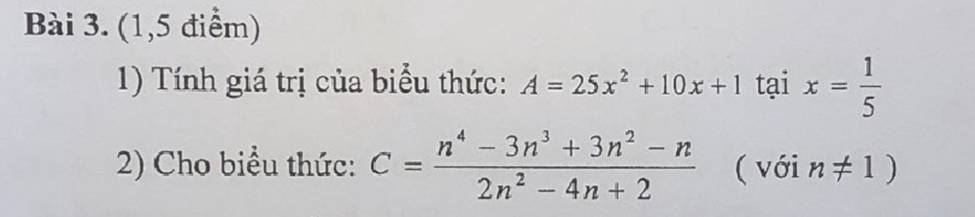Giai dùm mình với ạ

1) \(A=25x^2+10x+1\)

\(A=5x^2+2.5.10x+1\)

\(A=5x^2+100x+1\)

\(A=\left(5x+1\right)^2\) 

Thay \(x=\dfrac{1}{5}\)  vào biểu thức \(\left(5x+1\right)^2\)

\(\left(5x+1\right)^2\)

= \(\left(5.\dfrac{1}{5}+1\right)^2\)

= \(2^2=4\)

Nếu sai thì cho mình xin lỗi nhé

2) Bài này mình không biết làm 

2) yêu cầu là gì em?

1 B

2 C

3 A

4 A

5 C

6 C

7 D

8 B

9 D

10 B

11 C

12 D

13 B

14 A

15 A

16 C

17 A

18 B

19 B

20 A

21 A

22 D

23 C

24 A

25 B

26 A

27 B

28 A

29 C

30 D

Quy tắc đọc với s bạn tự xem lại kiến thức nhé

51 later

52 crossword

53 on

54 from

55 arrange 

56 instead

57 horizontal

58 invented

59 was

60 first

5/ \(10x+3-5x\le14x+12\)
<=>\(10x-5x-14x\le12-3\)
<=>\(-9x\le9\)
<=>\(x\ge-1\)
Vậy bất phương trình có nghiệm là \(x\ge-1\)

6/\(\left(3x-1\right)< 2x+4\)
<=>\(3x-2x< 4+1\)
<=> x<5
Vậy tập nghiệm của bất phương trình là x<5

9/ \(\left(x-1\right)\left(x+2\right)>\left(x-1\right)^2+3\)
<=>\(x^2+2x-x-2>x^2-2x+1+3\)
<=> \(x^2+2x-x-x^2-2x>1+3+2\)
<=>\(-x>6\)
<=> x<-6
Vậy nghiệm của bất pt là X<-6

`(1+2cosx)(3-cosx)=0`

\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\cosx=3\left(L\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2\pi}{3}+k2\pi\\x=\dfrac{-2\pi}{3}+k2\pi\end{matrix}\right.\\ \Leftrightarrow x=\dfrac{2\pi}{3}+k\pi\)

`(k \in ZZ)`

\(\Leftrightarrow\left[{}\begin{matrix}1+2\cos x=0\\3-\cos x=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\cos x=-\dfrac{1}{2}\\\cos x=3\end{matrix}\right.\)

Mà \(-1\le\cos x\le1\)

\(\Rightarrow\cos x=-\dfrac{1}{2}\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\pi+k2\pi\\x=\dfrac{4}{3}\pi+k2\pi\end{matrix}\right.\)

Vậy ...