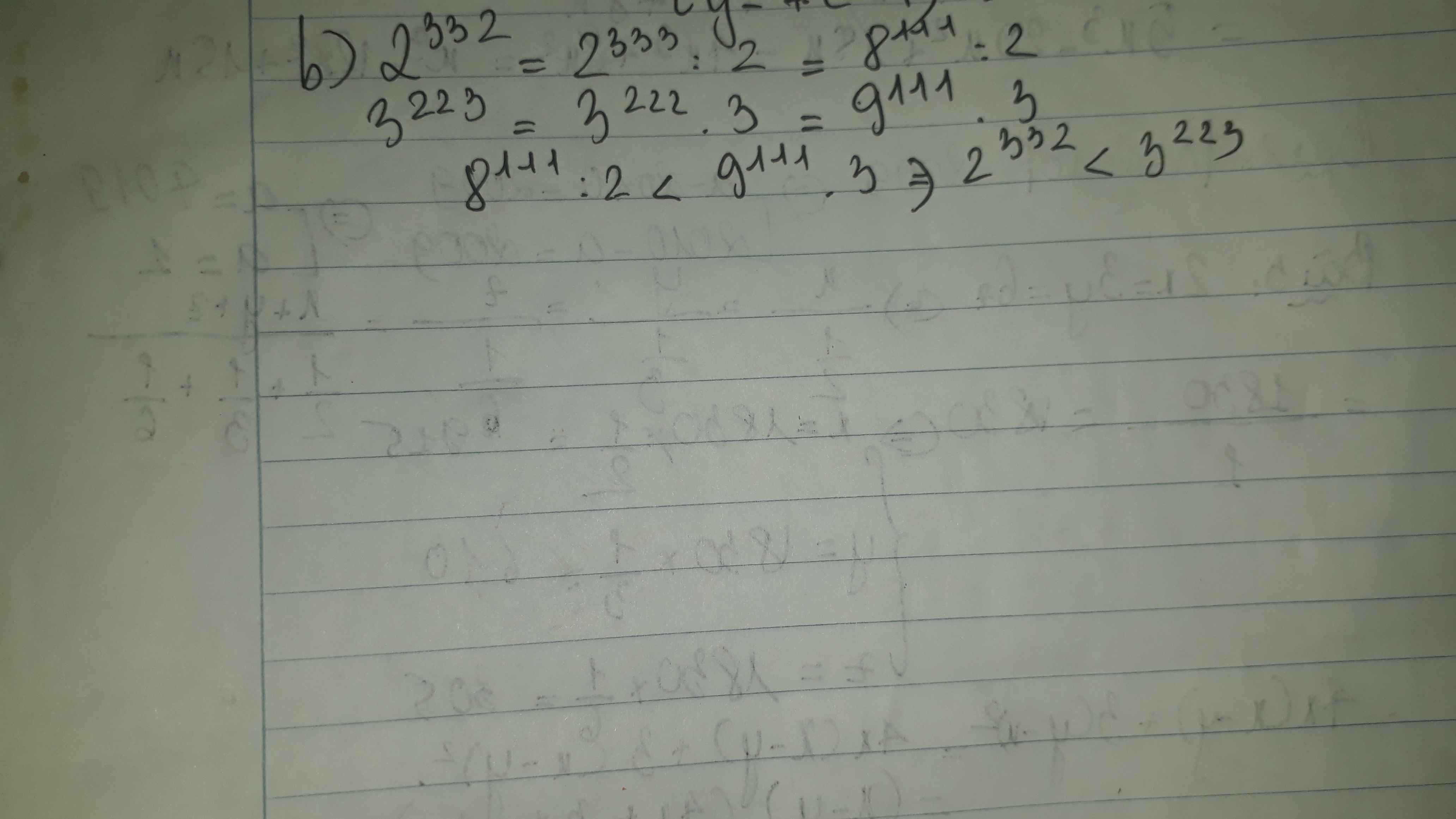Cho A = 20 + 21 + 22 + 23 + ..... + 22009 + 22010 . Tìm số dư khi chia A cho 3

Những câu hỏi liên quan
Cho A = 1 + 2 + 2 2 + . . . + 2 2009 + 2 2010 . Tìm số dư khi chia A cho 7
Ta có: A = 1 + 2 + 2 2 + . . . + 2 2009 + 2 2010
= 1 + 2 ( 1 + 2 + 2 2 ) + ... + 2 2008 ( 1 + 2 + 2 2 )
= 1 + 2 ( 1 + 2 + 4 ) + ... + 22008 ( 1 + 2 + 4 )
= 1 + 2 . 7 + ... + 2 2008 . 7 = 1 + 7 ( 2 + ... + 2 2008 )
Mà 7 ( 2 + ... + 2 2008 ) ⋮ 7. Do đó: A chia cho 7 dư 1.
Đúng 0
Bình luận (0)
Cho A = 1 + 2 + 2 2 + ... + 2 2009 + 2 2010 . Tìm số dư khi chia A cho 7.
Ta có: A = 1 + 2 + 2 2 + 2 3 + ... + 2 2008 + 2 2009 + 2 2010
= 1 + 2 ( 1 + 2 + 22 ) + ... + 2 2008 ( 1 + 2 + 22 )
= 1 + 2 ( 1 + 2 + 4 ) + ... + 2 2008 ( 1 + 2 + 4 )
= 1 + 2 . 7 + ... + 2 2008 . 7 = 1 + 7 ( 2 + ... + 2 2008 )
Mà 7 ( 2 + ... + 2 2008 ) ⋮ 7. Do đó: A chia cho 7 dư 1.
Đúng 0
Bình luận (0)
Chứng minh: A = 21 22 23 24 ... 22010 chia hết cho 3 và 7 Chứng minh: A = 21 22 23 24 ... 22010 chia hết cho 3 và 7
Ta có :
\(A=2+2^2+2^3+2^4...2^{2010}\)\(^0\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{2009}\left(1+2\right)\)
\(=2.3+2^3.3+....+2^{2009}.3\)
\(=3\left(2+2^3+....+2^{2009}\right)⋮3\)
Ta có :
\(2+2^2+2^3+2^4+....+2^{2010}\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2008}\left(1+2+2^2\right)\)
\(=2.7+2^4.7+....+2^{2008}.7\)
\(=7\left(2+2^4+....+2^{2008}\right)⋮7\)
Vậy \(2^1+2^2+2^3+2^4+...+2^{2010}⋮3\) và \(7\)
a,chứng minh:A=21+22+23+24+....22010 chia het cho 3 va 7
a,A=(2+22)+(23+24)+...+(22009+22010)
A=(1+2)(2+23+...+22009)=3(2+...+22009)⋮3
A=(2+22+23)+...+(22008+22009+22010)
A=(1+2+22)(2+...+22008)=7(2+...+22008)⋮7
Đúng 0
Bình luận (0)
a) Tính M = 22010 - ( 22009 + 22008 + ..... + 21 + 20 )
b) So sánh: 2332 và 3223
Tính: M = 22010 - (22009 + 22008 + ... + 21 + 20)
Đặt A = 22009 + 22008 + ... + 21 + 20. Khi đó, M = 22010 - A
Ta có 2A = 22010 + 22009 + ... + 22 + 21.
Suy ra 2A - A = 22010 - 20 = 22010 - 1.
Do đó M = 22010 - A = 22010 - (22010 - 1) = 22010 - 22010 + 1 = = 1.
Đúng 0
Bình luận (0)
M=2^2010-(2^2009+2^2008+2^2007+...+2^1+2^0)
M=22010-22009-22008-22007-...-21-20
=>2M=22011-22010-22009-22008-...-22-21
=>2M-M=22011-22010-22009-22008-...-22-21-(22010-22009-22008-22007-...-21-20)
=>M=22011-22010-22009-22008-...-22-21-22010+22009+22008+22007+...+21+20
=22011-22010-22010+20
=22011-2.22010+1
=22011-22011+1
=1
vậy M=1
A=20+21+22+23+24+.........+22015+22016
Tìm số dư khi chia A cho 7.![]()
A=(1+2+2^2)+2^3(1+2+2^2)+...+2^2013(1+2+2^2)+2^2016
=7(1+2^3+...+2^2013)+2^2016
Vì 2^2016 chia 7 dư 1
nên A chia 7 dư 1
Đúng 0
Bình luận (0)
Số dư của A = 20 + 21 + 22 + 23 + .......... + 2100 khi chia cho 100 là: ................
Ta có A=20+21+22+23+...2100
2A=21+22+...+2101
2A-A=(21+22+...+2100)-(20+21+...+2100)
A=2101-1
Mà 2101-1=(........02)-1=........01 chia 100 dư 1
Chúc bạn học tốt.
Đúng 0
Bình luận (0)
Giúp vs
Bài 1. Tìm x biết
a) (x+3)3=640000
b) 275.3x=910
c) (1/33.9).3x=27
d) 85.4x=221
Bài 2. Tính
M=22010-(22009+22008+...+21+20)
chứng minh :A=21+22+23+...+22010 chia hết cho 7
viết cả bài làm
mình đang vội lắm rồi
\(A=2\left(1+2+2^2\right)+...+2^{2008}\left(1+2+2^2\right)\)
\(=7\left(2+...+2^{2008}\right)⋮7\)
Đúng 0
Bình luận (0)