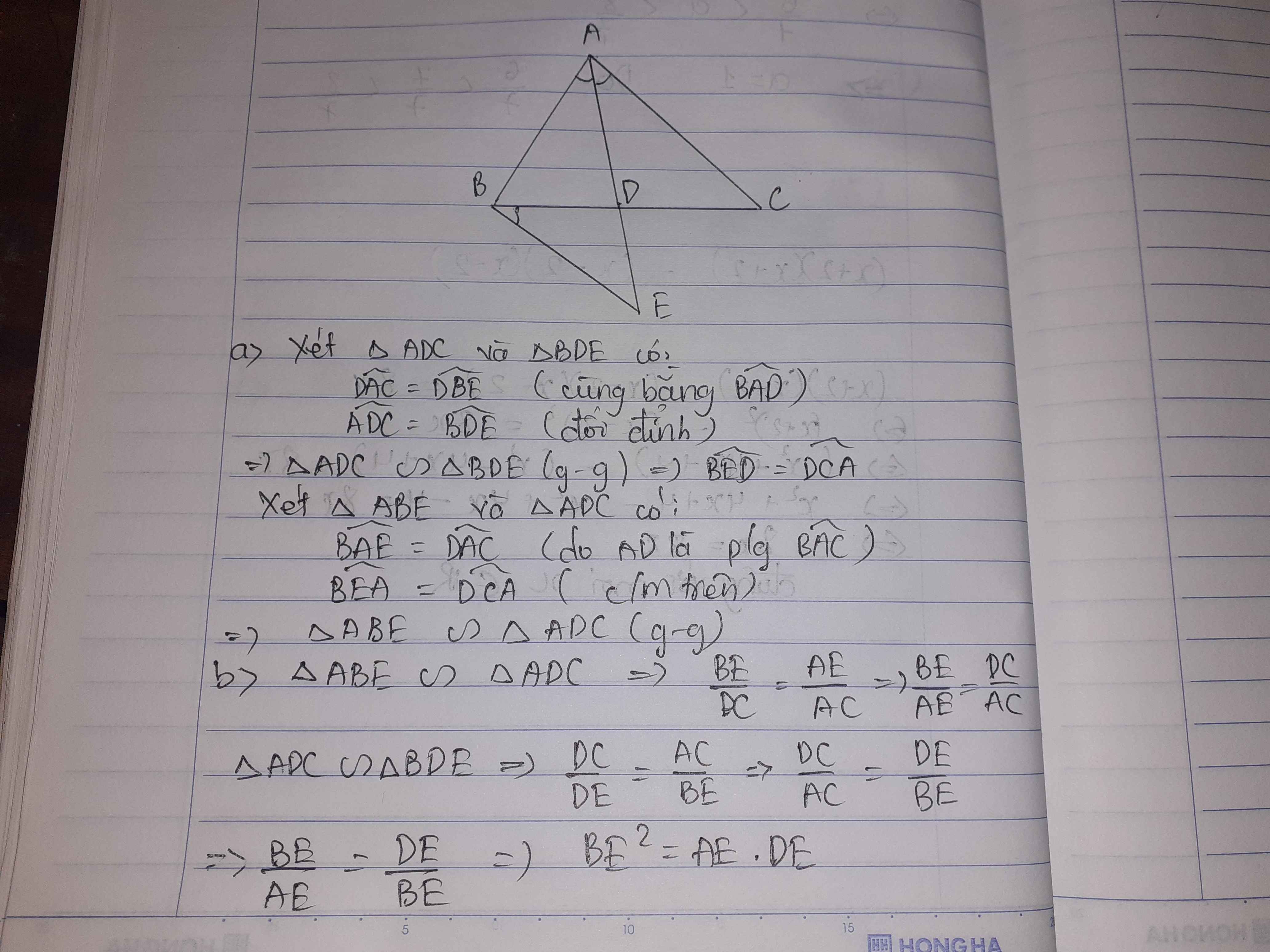
cho tam giác ABC phân giác AD qua B kẻ tia phân giác Bx sao cho góc CBX= góc BAD .tia Bx cắt AD ở E .a, cm tam giác ABE đồng dạng tam giác ADC . b, Be^2=AD.AE

Những câu hỏi liên quan
Cho tam giác ABC phân giác AD . Qua B kẻ Bx sao cho góc CBx = góc BAD . Tia Bx cắt DA ở E ( Bx và BA nằm trên 2 nửa mặt phẳng bờ BC ) CMR
a) Tam giác ABE đồng dạng tam giác ADC
b) BE2 = AD.AE
Cho tam giác ABC , phân giác AD . Qua B kẻ tia Bx sao cho góc CBx = góc BAD . Tia Bx cắt tia AD ở E. Chứng minh ;
a) Tam giác ABE đồng dạng tam giác ADC
b) BE2 = AD . AE
MÌNH ĐANG CẦN GẤP NHÉ
HÌNH TỰ KẺ NHA
1a) trong tam giác ADB có ADC là góc ngoài tại đỉnh D
=>góc ADC = góc BAD + góc ABD
mà góc BAD = góc DBE
=>góc ADC = góc ABD + góc DBE
=>góc ADB = góc ABE
Xét tam giác ADC va tam giác ABE
Góc BAD = góc CAD(AD là p/g tại đỉnh A)
góc ABE = góc ADC(cmt)
=> tam giác ABE đồng dạng với tam giác ADC(g.g)
1b) Xét tam giac AEB và tam giác BED
góc E chung
góc DBE = góc DAB(gt)
=>tam giác ABE đồng dạng vói tam giác BDE(g.g)
=>BE/DE = AE/BE
=>BE.BE=DE.AE
hayBE^2=DE.AE
Đúng 0
Bình luận (0)
Cho tam giác ABC , phân giác AD . Qua B kẻ Bx sao cho góc CBx = góc BAD . Tia Bx cắt DA ở E ( Bx và BA nằm trên 2 nửa mặt phẳng bờ BC) . CMR
a) Tam giác ABE đồng dạng tam giác ADC
b) \(BE^2\) = AD . AE
a: Xét ΔABE và ΔADC có
góc BAE=góc DAC
góc AEB=góc ACD
=>ΔABE đồng dạng với ΔADC
b: ΔABE đồng dạng với ΔADC
=>AE/AC=AB/AD
=>AE*AD=AB*AC=BE^2
Đúng 0
Bình luận (0)
cứuuuuuuuuuuuuuuuuuuuuuuuuuu
cho tam ABC, phân giác AD. Qua B kẻ tia Bx sao cho CBx=BAD. Tia Bx cắt tia AD ở E. Chứng minh:
a, tam giác ABE~tam giác ADC.
b, BE^2 = DE,AE
đọc đề bài mà tui chẳng hiểu cái gì cả
Đúng 0
Bình luận (0)
cho tam ABC, phân giác AD. Qua B kẻ tia Bx sao cho CBx=BAD. Tia Bx cắt tia AD ở E. Chứng minh: a, tam giác ABE~tam giác ADC. b, BE^2 = DE,AE
Cho tam giác ABC phân giác ad,qua b kẻ Bx sao cho CBx=ABD tia Bé cắt tia AD ở E Chứng minh BE^2=AD.AE
Xét ΔEBD và ΔEAB có
góc EBD=góc EAB
góc E chung
=>ΔEBD đồng dạng vơi ΔEAB
=>EB/EA=ED/EB
=>EB^2=EA*ED
Đúng 0
Bình luận (0)
Cho △ABC, phân giác AD. Qua B kẻ Bx sao cho góc CBx = góc BAD. Tia Bx cắt DA ở E (Bx và BA nằm trên hai nửa mặt phẳng bờ là BC). Chứng minh
a. △ABE đòng dạng với △ADC
b. \(^{BE^2}\) = DE.AE
a) Xét ΔABE và ΔADC có
\(\widehat{BAE}=\widehat{DAC}\)(hai góc đối đỉnh)
\(\widehat{AEB}=\widehat{ACD}\)(ΔDBE\(\sim\)ΔDAC)
Do đó: ΔABE\(\sim\)ΔADC(g-g)
Đúng 0
Bình luận (0)
b) Xét ΔEBD và ΔEAB có
\(\widehat{BEA}\) chung
\(\widehat{EBD}=\widehat{EAB}\)(gt)
Do đó: ΔEBD\(\sim\)ΔEAB(g-g)
Suy ra: \(\dfrac{BE}{AE}=\dfrac{DE}{BE}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(BE^2=DE\cdot AE\)
Đúng 0
Bình luận (0)
cho tam giác ABC, đường phân giác AD, trên nửa mặt phẳng bờ BC ko chứa A vẽ tia Bx sao cho góc BAD =góc CBx. gọi M là giao điểm của AD và Bx
a)c/m tam giác MBD đồng dạng vs tam giác MAB
b)vẽ tia phân giác góc ABC cắt AD ở I .C/M tam giác MBI cân
c)từ M vẽ đường thẳng vng góc vs MA cắt đường cao xuất phát từ A của tam giác ABC tại E ,cắt BC tại F. c/m tam giác EIF vuông
a) Xét tam giác MBD và tam giác MAB:
\(\widehat{DMB}chung.\)
\(\widehat{DBM}=\widehat{BAM}\left(\widehat{CBx}=\widehat{BAD}\right).\)
=> Tam giác MBD \(\sim\) Tam giác MAB (g - g).
Đúng 3
Bình luận (1)
Cho ∆ABC, phân giác AD. Qua B kẻ tia Bx sao cho góc CBx= góc ABD. Tia Bx cắt tia AD ở E. Chứng minh: BE^2 = AE.DE
Xét ΔEBD và ΔEAB có
góc EBD=góc EAB
góc E chung
=>ΔEBD đồng dạng vơi ΔEAB
=>EB/EA=ED/EB
=>EB^2=EA*ED
Đúng 1
Bình luận (0)