a) ta có: A = 3^0 + 3^1 + 3^2 + ...+ 3^100

=> 3A = 3^1 + 3^2 + 3^3 + ...+ 3^101

=> 3A-A = 3^101 - 3^0

2A = 3^101 - 1

\(A=\frac{3^{101}-1}{2}\)

b) D = 1 - 5 + 5^2 - 5^3 + ...+ 5^98 - 5^99

=> 5D = 5 - 5^2 + 5^3 - 5^4+...+ 5^99 - 5^100

=> 5D+D = -5^100 + 1

6D = -5^100 + 1

\(D=\frac{-5^{100}+1}{6}\)

M=2+2^3+2^5+2^7+...+2^99(1)

=>4M=2^3+2^5+...+2^101(2)

Lấy (2)-(1) ta có :

=>3M=2^101-2

=>M=(2^101-2)/3

ko bt làm

câu dễ thế mà cũng phải hỏi à hải anh.

ai giúp mk đi mà mk tick cho tick cho 2 tick luôn

dễ sao bạn ko làm đi!!!

    1. Phương pháp 1: ( Hình 1)

        Nếu  thì ba điểm A; B; C thẳng hàng.

    2. Phương pháp 2: ( Hình 2)

        Nếu AB // a và AC // a thì ba điểm A; B; C thẳng hàng.

       (Cơ sở của phương pháp này là: tiên đề Ơ – Clit- tiết 8- hình 7)

    3. Phương pháp 3: ( Hình 3)

        Nếu AB  a ; AC  A thì ba điểm A; B; C thẳng hàng.

        ( Cơ sở của phương pháp này là: Có một và chỉ một đường thẳng

        a^’ đi qua điểm O và vuông góc với đường thẳng a cho trước

        - tiết 3 hình học 7)

        Hoặc A; B; C cùng thuộc một đường trung trực của một

        đoạn thẳng .(tiết 3- hình 7)

    4. Phương pháp 4: ( Hình 4)

        Nếu tia OA và tia OB là hai tia phân giác của góc xOy

        thì ba điểm O; A; B thẳng hàng.

        Cơ sở của phương pháp này là:                                                        

        Mỗi góc có một và chỉ một tia phân giác .

     * Hoặc : Hai tia OA và OB cùng nằm trên nửa mặt phẳng bờ chứa tia Ox ,

                   thì ba điểm O, A, B thẳng hàng.

    5. Nếu K là trung điểm BD, K^’ là giao điểm của BD và AC. Nếu K^’

       Là trung điểm BD  thì K^’  K thì A, K, C thẳng hàng.

      (Cơ sở của phương pháp này là: Mỗi đoạn thẳng chỉ có một trung điểm)

C. Các ví dụ minh họa cho tùng phương pháp:

                                                                Phương pháp 1

    Ví dụ 1. Cho tam giác ABC vuông ở A, M là trung điểm AC. Kẻ tia Cx vuông góc CA

                     (tia Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC). Trên tia Cx lấy điểm

                     D sao cho CD = AB.

                     Chứng minh ba điểm B, M, D thẳng hàng.

     Gợi ý: Muốn B, M, D thẳng hàng cần chứng minh

               Do nên cần chứng minh

BÀI GIẢI:

               AMB và CMD có:                                                       

                   AB = DC (gt).

                    MA = MC (M là trung điểm AC)                                              

               Do đó: AMB = CMD (c.g.c). Suy ra:

               Mà   (kề bù) nên .

               Vậy ba điểm B; M; D thẳng hàng.

    Ví dụ 2. Cho tam giác ABC. Trên tia đối của AB lấy điểm D mà  AD = AB, trên tia đối

                     tia AC lấy điểm E mà AE = AC. Gọi M; N lần lượt là các điểm trên BC và ED

                      sao cho CM = EN.

                    Chứng minh ba điểm M; A; N thẳng hàng.

Gợi ý: Chứng minh  từ đó suy ra ba điểm M; A; N thẳng hàng.

BÀI GIẢI (Sơ lược)

          ABC = ADE (c.g.c)

          ACM = AEN (c.g.c)

          Mà  (vì ba điểm E; A; C thẳng hàng) nên

Vậy ba điểm M; A; N thẳng hàng (đpcm)

BÀI TẬP THỰC HÀNH CHO PHƯƠNG PHÁP 1

Bài 1: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AC, trên tia đối

          của tia AC lấy điểm E sao cho AE = AB. Gọi M, N lần lượt là trung điểm của BE và

          CD.

          Chứng minh ba điểm M, A, N thẳng hàng.

Bài 2: Cho tam giác ABC vuông ở A có . Vẽ tia Cx  BC (tia Cx và điểm A ở

          phía ở cùng phía bờ BC), trên tia Cx lấy điểm E sao cho CE = CA. Trên tia đối của tia

          BC lấy điểm F sao cho BF = BA.

          Chứng minh ba điểm E, A, F thẳng hàng.

Bài 3: Cho tam giác ABC cân tại A, điểm D thuộc cạnh AB. Trên tia đối của tia CA lấy điểm

          E sao cho CE = BD. Kẻ DH và EK vuông góc với BC (H và K thuộc đường thẳng BC)

          Gọi M là trung điểm HK.

          Chứng minh ba điểm D, M, E thẳng hàng.

Bài 4: Gọi O là trung điểm của đoạn thẳng AB. Trên hai nửa mặt phẳng đối nhau bờ AB, kẻ

          Hai tia Ax và By sao cho .Trên Ax lấy hai điểm C và E(E nằm giữa A và C),

          trên By lấy hai điểm D và F ( F nằm giữa B và D) sao cho AC = BD, AE = BF.

          Chứng minh ba điểm C, O, D thẳng hàng , ba điểm E, O, F thẳng hàng.

Bài 5.Cho tam giác ABC . Qua A vẽ đường thẳng xy // BC. Từ điểm M trên cạnh BC, vẽ các

          đường thẳng song song AB và AC, các đường thẳng này cắt xy theo thứ tự tại D và E.

          Chứng minh các đường thẳng AM, BD, CE cùng đi qua một điểm.

                                                              PHƯƠNG PHÁP 2

    Ví dụ 1: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AC, AB. Trên

                  Các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung  

                 điểm BD và N là trung điểm EC.

                  Chứng minh ba điểm E, A, D thẳng hàng.

Hướng dẫn: Xử dụng phương pháp 2                                            

                  Ta chứng minh AD // BC và AE // BC.

BÀI GIẢI.

                 BMC và DMA có:

                   MC = MA (do M là trung điểm AC)

                    (hai góc đối đỉnh)

                   MB = MD (do M là trung điểm BD)

                  Vậy: BMC = DMA (c.g.c)

                   Suy ra: , hai góc này ở vị trí so le trong nên BC // AD (1)

                   Chứng minh tương tự : BC // AE (2)

                   Điểm A ở ngoài BC có một và chỉ một đường thẳng song song BC nên từ (1)

                   và (2) và theo Tiên đề Ơ-Clit suy ra ba điểm E, A, D thẳng hàng. 

   Ví dụ 2: Cho hai đoạn thẳng  AC và BD cắt nhau tai trung điểm O của mỗi đoạn. Trên tia

                 AB lấy lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho

                 D là trung điểm AN. 

1/ \(x^3+2=3\sqrt[3]{3x-2}\)

Đặt \(\sqrt[3]{3x-2}=a\) thì ta có hệ

\(\hept{\begin{cases}x^3+2-3a=0\\a^3+2-3x=0\end{cases}}\)

Lấy trên - dưới ta được

\(x^3-a^3+3x-3a=0\)

\(\Leftrightarrow\left(x-a\right)\left(x^2+ax+a^2+3\right)=0\)

\(\Leftrightarrow x=a\)

\(\Leftrightarrow x=\sqrt[3]{3x-2}\)

\(\Leftrightarrow x^3-3x+2=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=-2\end{cases}}\)

2/ \(x+\sqrt{5-x^2}+x\sqrt{5-x^2}=5\)

Đặt \(\sqrt{5-x^2}=a\ge0\) thì ta có hệ

\(\hept{\begin{cases}x+a+ax=5\\a^2+x^2=5\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x+a+ax=5\\\left(a+x\right)^2-2ax=5\end{cases}}\)

Tới đây thì đơn giản rồi. Đặt \(\hept{\begin{cases}a+x=S\\ax=P\end{cases}}\) giải tiếp sẽ ra

1.

Số thừa số sẽ là :

lấy  : ( 2009 - 9 ) : 10 + 1 = 201 ( thua so )

Ta thấy rằng : 9 x 9 = 81  

Vậy nên là : 200 thừa số sẽ có tích có chữ số tận cùng là : 1

=> khi nhận thừa số thứ 201 thì tích có chữ số tận cùng là : 9

2.

 số chia hết cho cả 2 và 5 => số đó phải chia hết cho 10

Số lớn nhất có 4 chữ số chia hết cho 10 là 9990

Số nhỏ nhất có 4 chữ số chia hết cho 10 là 1000

   Hai số liên tiếp hơn kém nhau 10 đơn vị .

  có tất cả số số có 4 chữ số chia hết cho cả 2 và 5  hoặc chia hết cho 10 là :

                          (9990-1000):10+1=900(số)

             Vậy có tất cả 900 số .

3.

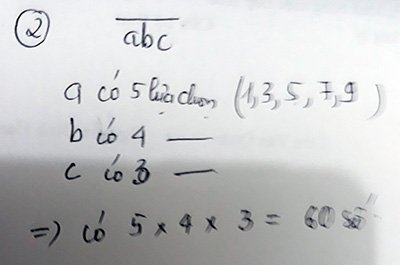
4.

4/5 = 1608/2010

=> a lớn nhất là 1607

Vậy a lớn nhất là 107

thoi minh luoi lam minh ko giai het duoc dau

- Đề bài bài 4 nhầm nha. 

- Phải là : 19^x + 5^y + 1980z = 1975^430 + 2004

- Bạn Khoi giai giúp mk đi. Please !!!

chữ số tạn cùng là chữ số 0

nếu tính nhanh thì lấy 2015*2016=4062240 có tận cùng là chữ số 0