Cho góc xOy=60o vẽ tia phân giác Oz, trên Oz lấy điểm M, vẽ MA vuông góc với Ox; MB vuông góc với Oy.
a) Chứng minh: ΔOAB đều
b) MA cắt Oy tại C và MB cắt Ox tại D.Chứng minh: ΔMCD cân và ΔOCD đều
c) Chứng minh: AB//CD
Mình đang cần gấp thanks m.n
Vẽ góc xOy và Oz là tia phân giác của góc xOy, trên tia Oz lấy điểm M. Vẽ MA vuông góc với Oy, vẽ MB vuông góc với Oy. Chứng minh MA = MB
Xét △AOM và △BOM
Ta cs: OM cạnh chung
góc O1 = góc O2
góc A = góc B = 90 độ
vậy △AOM = △BOM ( chgn )
=> AM = BM ( cặp cạnh tương ứng )
vẽ góc xOy, Oz là tia phân giác của góc xOy, lấy điểm M bất kì thuộc Oz. Từ M kẻ MA vuông góc với Ox,MB vuông góc với Oy. Chứng minh MA=MB
Vì Oz là tia phân giác của góc xOy
=>góc AOM = góc BOM
VÌ MA\(\perp\)Ox =>góc MAO=90o
MB \(\perp\)Oy =>góc MBO=90o
Xét \(\Delta AOM\)và \(\Delta BOM\)có:
Góc MAO= Góc MBO(Cùng bằng 90o)
OM:cạnh chung
Góc AOM = góc BOM
=>\(\Delta AOM=\Delta BOM\left(Ch-gn\right)\)
=>MA=MB(các cạnh tương ứng)
Cho góc xOy (khác với góc bẹt ) vẽ tia phân giác Ox của góc xOy . Lấy điểm M thuộc tia Oz . Từ M kẻ MA vuông góc với Ox . MB vuông góc với Oy .
a) Cmr OA = OB
b) Lấy điểm C thuộc tia Oz . Cmr CA = CB
Cho góc xOy, kẻ tia phân giác Oz của xOy.Trên Ox lấy điểm A,trên Oy lấy điểm B sao cho OA=OB .Trên Oz lấy điểm M. Kẻ tia MH vuông góc Ox, MK vuông góc Oy ; Nối MA và MB . Chứng minh tam giác MAH=tam giác MBK. (cần vẽ hình và giải đáp ) giúp mik giải nhan :< !
Xét ΔOAM và ΔOBM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔOAM=ΔOBM
Suy ra: MA=MB
Xét ΔOKM vuông tại K và ΔOHM vuông tại H có
OM chung
\(\widehat{KOM}=\widehat{HOM}\)
Do đó;ΔOKM=ΔOHM
Suy ra: OH=OK
=>AH=BK
Xét ΔMAH vuông tại H và ΔMBK vuông tại K có
MA=MB
AH=BK
Do đó: ΔMHA=ΔMKB
Cho góc vuông xOy và Oz là tia phân giác. Gọi M là điểm tùy ý trên tia Oz (M không trùng với O). Vẽ MA vuông góc với Ox (A thuộc Ox). MB vuông góc với Oy (B thuộc Oy).
a)
Chứng minh OA = OB.
b) Trên đoạn thẳng AM lấy điểm I, nối I với O. Qua I vẽ tia IK (K thuộc MB ) sao cho góc AIO = KIO. Tính góc IOK
Cho Oz là tia phân giác của góc xOy. Lấy điểm M trên tia Oz và hai điểm A, B lần lượt trên các tia Ox, Oy sao cho MA vuông góc với Ox, MB vuông góc với Oy(H.4.50). Chứng minh rằng MA = MB.
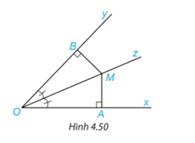
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)
Cho góc nhọn xOy, vẽ tia Oz là tia phân giác của góc xOy. Trên Oz lấy điểm A. Qua A kẻ đường thẳng d vuông góc với Oz cắt Ox, Oy tại M, N. Chứng minh tam giác OMA = Tam giác ONA
Vì Oz là phân giác xOy
=> xOz = zOy = xOy/2
Xét △OMA vuông tại M và △ONA vuông tại N
Có: xOz = zOy
Oz là cạnh chung
=> △OMA = △ONA ( cgv - gn)
Cho góc xOy có tia phân giác Oz. Trên Oz lấy điểm E, vẽ đường thẳng qua E vuông góc với Ox tại K, cắt Oy tại N. Vẽ đường thẳng qua E vuông góc với Oy tại H cắt Ox tại M. Chọn câu đúng
A. OK<OH,KN<HM
B. OK=OH,KN<HM
C. OK<OH,KN>HM
D. OK=OH,KN=HM
Cho góc vuông xoy và oz là tia phân giác. Từ một điểm A trên tia phân giác Oz, kẻ AB vuông góc với Ox, AC vuông góc với Oy ( B thuộc Ox, C thuộc Oy ) . lấy điểm M trên Ab , từ M vẽ một đường thẳng tạo với MO một góc bằng BMO cắt AC tại N . CM MON bằng 45 dộ
Tui là anti
Cho góc xOy có số đo bằng 120 độ có Oz là tia phân giác. Trên Oz lấy điểm A, qua A vẽ AB vuông góc với Ox (B thuộc Oz), vẽ AC vuông góc với Oy (C thuộc Oy). Chứng minh rằng tam giác ABC là một tam giác đều