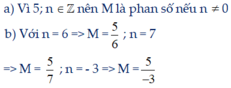Tìm GTNN của biểu thức A=|11m-5n| với m,n \(\in\) N*

Những câu hỏi liên quan
Tìm GTLN và GTNN của biểu thức \(\dfrac{5n+2}{2n+1}\) với \(n\in N\)*
Lời giải:
$\frac{5n+2}{2n+1}=\frac{2,5(2n+1)-0,5}{2n+1}=2,5-\frac{0,5}{2n+1}$
Để $\frac{5n+2}{2n+1}$ lớn nhất thì $\frac{0,5}{2n+1}$ nhỏ nhất
$\Leftrightarrow 2n+1$ lớn nhất
$\Leftrightarrow n$ lớn nhất. Trong tập số tự nhiên thì không tồn tại số tự nhiên lớn nhất nên không có GTLN
Để $\frac{5n+2}{2n+1}$ nhỏ nhất thì $\frac{0,5}{2n+1}$ lớn nhất
$\Leftrightarrow 2n+1$ nhỏ nhất $\Leftrightarrow n$ nhỏ nhất
Với $n\in\mathbb{N}^*$ thì $n$ nhỏ nhất bằng $1$
$\Rightarrow \frac{5n+2}{2n+1}$ min $=\frac{5.1+2}{2.1+1}=\frac{7}{3}$
Đúng 0
Bình luận (0)
Cho biểu thức:
A = \(\frac{5n-19}{n-4}\)
Tìm giá trị nguyên của n để biểu thức A có GTNN
cho biểu thức: P = m2- 4mn+ 5n2+ 10m -22n +32
Tìm m, n để P đạt GTNN. Tìm GTNN đó
Tìm GTNN của biểu thức A = giá trị tuyệt đối của \(11^m-5^n\)với m,n \(\in\)N sao
Ta thấy \(11^m\) tận cùng bằng 1, còn \(5^n\) tận cùng bằng 5. Nếu \(11^m>5^n\) thì A tận cùng bằng 6, nếu \(11^m< 5^n\) thì A tận cùng bằng 4.
Ta chỉ ra trường hợp A = 4 : với m = 2, n = 3 thì A = |121-125| = 4
Như vậy min A = 4 khi chẳng hạn m = 2, n = 3
Đúng 0
Bình luận (0)
tìm GTNN của biểu thức A= |11m-5n| với m,n thuộc N*
Câu này ở đâu vậy bạn dạng này lạ quá
Đúng 0
Bình luận (0)
Biết (m,n)=1
a, Tìm (m+n, m\(^2\) +n\(^2\) )
b, Tìm (11m+2n, 18m+5n)
Biết (m,n)=1
a, Tìm (m+n, m\(^2\) +n\(^2\) )
b, Tìm (11m+2n, 18m+5n)
Cho biểu thức M = 5 n với n là số nguyên:
a) Số nguyên n phải có điều kiện gì để M là phân số?
b) Tìm phân số M, biết n = 6; n = 7; n = -3,
Ai giúp mình câu hỏi này với:
A=2n+2/n+2 + 5n+17/n+2 - 3n/n+2
a,Tìm điều kiện của n để biểu thức A là phân số.
b,Tìm các số n thuộc N để biểu thức A là số nguyên.