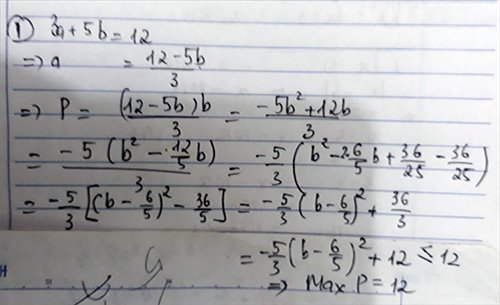Tim Min B = \(\frac{x^4+x^2+5}{x^4+2x^2+1}\)

Những câu hỏi liên quan
tim min y= (x^4+x^2+5)/(x^4+2x+1)
choP=(1/(x-2)-x^2/(8-x^3)*(x^2+2x+4)/(x+2)0/1/(x^2-4) tim DKXD va rut gon b tim Min p c tim x nguyen de p chia het cho x^2+1
1.tìm max A(frac{x}{x+2020})^2 với x0
2. tìm min C frac{left(4x+1right)left(4+xright)}{x} với x dương
3.cho 3a+5b12. tìmmin Bab
4.tìm min x^2-x+4+frac{1}{x^2-x}
5. cho x,y là 2 số thỏa mãn 2x^2+frac{1}{x^2}+frac{y}{4}4.tìm min max của xy
6. cho a,b0 và a+b1. tìm min Mleft(1+frac{1}{a}right)^2left(1+frac{1}{b}right)^2
Đọc tiếp
1.tìm max A=(\(\frac{x}{x+2020}\))\(^2\) với x>0
2. tìm min C= \(\frac{\left(4x+1\right)\left(4+x\right)}{x}\) với x dương
3.cho 3a+5b=12. tìmmin B=ab
4.tìm min \(x^2-x+4+\frac{1}{x^2-x}\)
5. cho x,y là 2 số thỏa mãn \(2x^2+\frac{1}{x^2}+\frac{y}{4}=4\).tìm min max của xy
6. cho a,b>0 và a+b=1. tìm min M=\(\left(1+\frac{1}{a}\right)^2\left(1+\frac{1}{b}\right)^2\)
tim x
a) / x+\(\frac{4}{15}\)/ - / -3,75 / = - / -2,15 /
b) / 4 + 2x / = - 4x
c) / x - 2 / - / 2x + 3 / = x - 1
d) / x - 2 / + / x - 3 / + / x - 4 / = 2
e) / 2x - 1 / + / 2x - 5 / = 4
a) /x+\(\frac{4}{15}\)/ - / -3,75/ = -2,15
=> \(\orbr{\begin{cases}x+\frac{4}{15}+3,75=-2,15\\x+\frac{4}{15}+3,75=2,15\end{cases}}\)
=> ....v.....v giải ra ( từng th )
bài khác tương tự
Đúng 0
Bình luận (0)
ai biet tra loi cho mik voi mik dag rat can gap
Đúng 0
Bình luận (0)
chi can lam bai c,d,e la duoc
nhung bai con lai mik tu lam duoc
Đúng 0
Bình luận (0)
Tìm min, max và tập giá trị của hàm số:
1, y = 3sin(2x + \(\frac{\pi}{4}\) ) - 1
2, y = -5\(cos^2\) x + 3
3, y = \(\frac{5}{3\cos x+4}\)
4, y = \(\sin^2\)x - 4sinx + 8
1: Ta có: \(-1<=\sin\left(2x+\frac{\pi}{4}\right)\le1\)
=>\(-3\le3\cdot\sin\left(2x+\frac{\pi}{4}\right)\le3\)
=>\(-3-1\le3\cdot\sin\left(2x+\frac{\pi}{4}\right)-1\le3-1\)
=>-4<=y<=2
=>Tập giá trị là T=[-4;2]
\(y_{\min}=-4\) khi \(\sin\left(2x+\frac{\pi}{4}\right)=-1\)
=>\(2x+\frac{\pi}{4}=-\frac{\pi}{2}+k2\pi\)
=>\(2x=-\frac34\pi+k2\pi\)
=>\(x=-\frac38\pi+k\pi\)
2: \(0\le cos^2x\le1\)
=>\(0\ge-5\cdot cos^2x\ge-5\)
=>\(0+3\ge-5\cdot cos^2x+3\ge-5+3\)
=>3>=y>=-2
=>Tập giá trị là T=[-2;3]
\(y_{\max}=3\) khi \(cos^2x=1\)
=>\(\sin^2x=0\)
=>sin x=0
=>\(x=k\pi\)
\(y_{\min}=-2\) khi \(cos^2x=0\)
=>cosx=0
=>\(x=\frac{k\pi}{2}\)
3: \(-1\le cosx\le1\)
=>\(-3\le3\cdot cosx\le3\)
=>\(-3+4\le3\cdot cosx+4\le3+4\)
=>\(1\le3\cdot cosx+4\le7\)
=>\(\frac51\ge\frac{5}{3\cdot cosx+4}\ge\frac57\)
=>\(\frac57\le y\le5\)
=>Tập giá trị là \(T=\left\lbrack\frac57;5\right\rbrack\)
\(y_{\min}=\frac57\) khi cosx=1
=>\(x=k2\pi\)
\(y_{\max}=5\) khi cosx=-1
=>\(x=\pi+k2\pi\)
4: \(y=\sin^2x-4\cdot\sin x+8\)
\(=\sin^2x-4\cdot\sin x+4+4\)
\(=\left(\sin x-2\right)^2+4\)
Ta có: \(-1\le\sin x\le1\)
=>\(-1-2\le\sin x-2\le1-2\)
=>\(-3\le\sin x-2\le-1\)
=>\(1\le\left(\sin x-2\right)^2\le9\)
=>\(5\le\left(\sin x-2\right)^2+4\le13\)
=>5<=y<=13
=>Tập giá trị là T=[5;13]
\(y_{\min}=5\) khi sin x-2=-1
=>sin x=1
=>\(x=\frac{\pi}{2}+k2\pi\)
\(y_{\max}\) =13 khi sin x-2=-3
=>sin x=-1
=>\(x=-\frac{\pi}{2}+k2\pi\)
Đúng 0
Bình luận (0)
Tìm min:
a, \(A=x+\frac{x-1}{\sqrt{x^2-2x}}\) với x>2
b, \(B=x\sqrt{x}-6x+13\sqrt{x}+\frac{4}{\sqrt{x}}\)
c,\(C=\frac{1-4\sqrt{x}}{2x+1}-\frac{2x}{x^2+1}\)
Tìm Min
\(A=x+\frac{x-1}{\sqrt{x^2-2x}}\left(x>2\right)\)
\(B=x\sqrt{x}-6x+13\sqrt{x}+\frac{4}{\sqrt{x}}\)
\(C=\frac{1-4\sqrt{x}}{2x+1}-\frac{2x}{x^2+1}\)
B1:Tìm min A= \(\frac{x^2-2x+9}{x^2}\)
B2: Tim min B=\(\frac{12}{x-1}\)+ \(\frac{x}{3}\) với x\(\ge\)1
B3: Tìm min C= /x-10/+/x-11/+/x-12/+/x-13/
Áp dụng bất đẳng thức AM-GM ta có :
\(B=\frac{12}{x-1}+\frac{x-1+1}{3}=\frac{12}{x-1}+\frac{x-1}{3}+\frac{1}{3}\ge2\sqrt{\frac{12}{x-1}\cdot\frac{x-1}{3}}+\frac{1}{3}=4+\frac{1}{3}=\frac{13}{3}\)
Dấu "=" xảy ra <=> \(\frac{12}{x-1}=\frac{x-1}{3}\Rightarrow x=7\left(x\ge1\right)\). Vậy MinB = 13/3
Tim min, max cua:
\(A=\frac{x^2+y^2}{x^2+2xy+y^2}\)
\(B=\frac{x^2}{x^4+1}\)
\(C=(x^2+\frac{1}{y^2})(y^2+\frac{1}{x^2})\)