cho hàm số y = x -2m - 1 ( m là tham số ')
a , xác định m để đồ thị đi qua gốc tọa độ 0
Những câu hỏi liên quan
cho đồ thị hàm số y=mx-2m-1(m khác 0)
xác định m để đồ thị hàm số đi qua gốc tọa độ O
Cho hàm số y = x - 2m - 1 (m là tham số)
a) Xác định m để đồ thị hàm số đi qua gốc tọa độ O
b) Tính theo m tọa độ các giao điểm A; B của đồ thị hàm số với các trục Ox; Oy. H là hình chiếu của O trên AB. Xác định giá trị của m để OH = căn2 /2
c) Tìm quỹ tích trung điểm I của đoạn thẳng AB
làm nhanh nhé cần gấp
Cho hàm số y=2mx-2m-1 (m khác 0)
a) Xác định m để đò thị hàm số đi qua gốc tọa độ O
b) Gọi A, B lần lượt là giao điểm của đồ thị hàm số với các trục Ox, Oy. Xác định m để diện tích tam giác AOB bằng 4( đvdt )
c) Chứng minh rằng đồ thị hàm số luôn đi qua 1 điểm cố định
sr nha em ko làm dc
Cho hàm số bậc nhất y = mx + (2m + 1)
a, Tìm giá trị của m để đồ thị hàm số đi qua gốc tọa độ 0
b, Cho m = 1, hãy vẽ đồ thị hàm số
c, Xác định m để đồ thị hàm số trên cắt đồ thị của hàm số y = 2x -1 tại một điểm nằm trên trục tung
a, hàm số đi qua gốc tọa độ O
\(\Rightarrow\) đồ thị hàm số có dạng \(y=x.z=mx+(2m+1)\Rightarrow 2m+1=0\)
\(\Rightarrow m=-\dfrac{1}{2}\)
b, khi \(m=1\Rightarrow y=x+3\)
Xét y=0 suy ra x=-3
suy ra lấy điểm A(-3,0)
Xét x=0 suy ra y=3
Lấy điểm B(0,3)
Nối A,B ta được đồ thị cần vẽ
c, đồ thị hàm số trên cắt đồ thị hàm số y=2x-1 tại 1 điểm trên trục tung suy ra gọi điểm đó là M ta có ( giao của 2 đồ thị nha)
M có hoành độ =0
thay vào 2 hàm số trên suy ra:
\(\hept{\begin{cases}y=2m+1\\y=-1\end{cases}\Rightarrow2m+1=-1\Rightarrow m=-1}\)
Xong rồi bạn nha!
Đúng 1
Bình luận (0)
quên mất kí hiệu A, B trên hình minh họa -_-
Đúng 0
Bình luận (0)
kí hiệu trên hình cũng sai luôn y=x+3 nha
Bạn tự sửa nha
Đúng 0
Bình luận (0)
cho hàm số y (m-1)x + m - 5a) xác định m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3b) xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -1c) xác định m để đồ thị hàm số đi qua gốc tọa độ
Đọc tiếp
cho hàm số y = (m-1)x + m - 5
a) xác định m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3
b) xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -1
c) xác định m để đồ thị hàm số đi qua gốc tọa độ
a: Thay x=0 và y=3 vào y=(m-1)x+m-5, ta được:
\(0\cdot\left(m-1\right)+m-5=3\)
=>m-5=3
=>m=8
b: Thay x=-1 và y=0 vào y=(m-1)x+m-5, ta được:
\(-\left(m-1\right)+m-5=0\)
=>-m+1+m-5=0
=>-4=0(vô lý)
c: Thay x=0 và y=0 vào y=(m-1)x+m-5, ta được:
\(0\left(m-1\right)+m-5=0\)
=>m-5=0
=>m=5
Đúng 1
Bình luận (0)
Cho hàm số y = (m+1)x − 2m+1 (d)
a) Xác định m để đường thẳng (d) đi qua gốc tọa độ.
b) Tìm m để đường thẳng (d) đi qua A(3; 4).Vẽ đồ thị với m vừa tìm được.
c) Tìm tọa độ giao điểm của đường thẳng vừa vẽ với đường thẳng (d’): y = −2x + 4
\(a,\Leftrightarrow A\left(0;0\right)\in\left(d\right)\Leftrightarrow-2m+1=0\Leftrightarrow m=\dfrac{1}{2}\\ b,\Leftrightarrow x=3;y=4\Leftrightarrow3\left(m+1\right)-2m+1=4\\ \Leftrightarrow3m+3-2m+1=4\\ \Leftrightarrow m=0\Leftrightarrow\left(d\right):y=x+1\\ c,\text{PT hoành độ giao điểm: }x+1=-2x+4\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow B\left(1;2\right)\\ \text{Vậy }B\left(1;2\right)\text{ là giao 2 đths}\)
Đúng 1
Bình luận (0)
Cho hàm số y=(2m-1)x+m-1.Xác định m để
a)Hàm số nghịch biến trong R
b) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ -1
c)Đồ thị hàm số đi qua điểm M(1;4).Khi đó vẽ đồ thị hàm số.Tính khoảnh cách từ gốc tọa độ O đến đường thẳng đó.
a: Để hàm số y=(2m-1)x+m-1 nghịch biến trên R thì 2m-1<0
=>2m<1
=>\(m< \dfrac{1}{2}\)
b: Thay x=-1 và y=0 vào y=(2m-1)x+m-1, ta được:
-(2m-1)+m-1=0
=>-2m+1+m-1=0
=>-m=0
=>m=0
c: Thay x=1 và y=4 vào y=(2m-1)x+m-1, ta được:
2m-1+m-1=4
=>3m-2=4
=>3m=6
=>m=2
Khi m=2 thì \(y=\left(2\cdot2-1\right)x+2-1=3x+1\)
vẽ đồ thị:
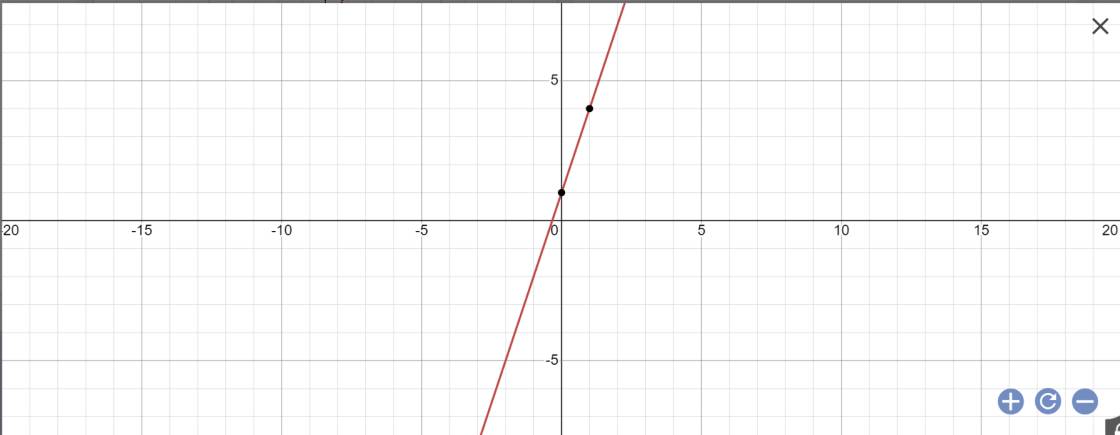
y=3x+1
=>3x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng 3x-y+1=0 là:
\(d\left(O;3x-y+1=0\right)=\dfrac{\left|0\cdot3+0\cdot\left(-1\right)+1\right|}{\sqrt{3^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{10}}\)
Đúng 0
Bình luận (0)
Cho hàm số y = m + 1 x - 2 m + 1 x - 1 (m là tham số) có đồ thị (G).
Xác định m để đồ thị (G) đi qua điểm (0; -1).
Cho hàm số y=(2m-1)x+m-1.Xác định m để:
a)Hàm số nghịch biến trong R
b)Đồ thị hàm số cắt trục hoành tại điểm tại điểm có hoành độ -1
c)Đồ thị hàm số đi qua điểm M(1;4).Tính khoảng cách từ gốc tọa độ O đến đường thẳng đó
a: Để hàm số nghịch biến trên R thì 2m-1<0
=>2m<1
=>\(m< \dfrac{1}{2}\)
b; Thay x=-1 và y=0 vào y=(2m-1)x+m-1, ta được:
\(\left(-1\right)\left(2m-1\right)+m-1=0\)
=>-2m+1+m-1=0
=>-m=0
=>m=0
c: Thay x=1 và y=4 vào y=(2m-1)x+m-1, ta được:
\(1\left(2m-1\right)+m-1=4\)
=>2m-1+m-1=4
=>3m=6
=>m=2
Khi m=2 thì \(y=\left(2\cdot2-1\right)x+2-1=3x+1\)
=>3x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng 3x-y+1=0 là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot3+0\cdot\left(-1\right)+1\right|}{\sqrt{3^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{10}}\)
Đúng 1
Bình luận (0)