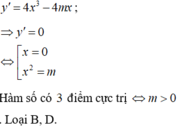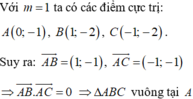Tìm cực trị của các hàm số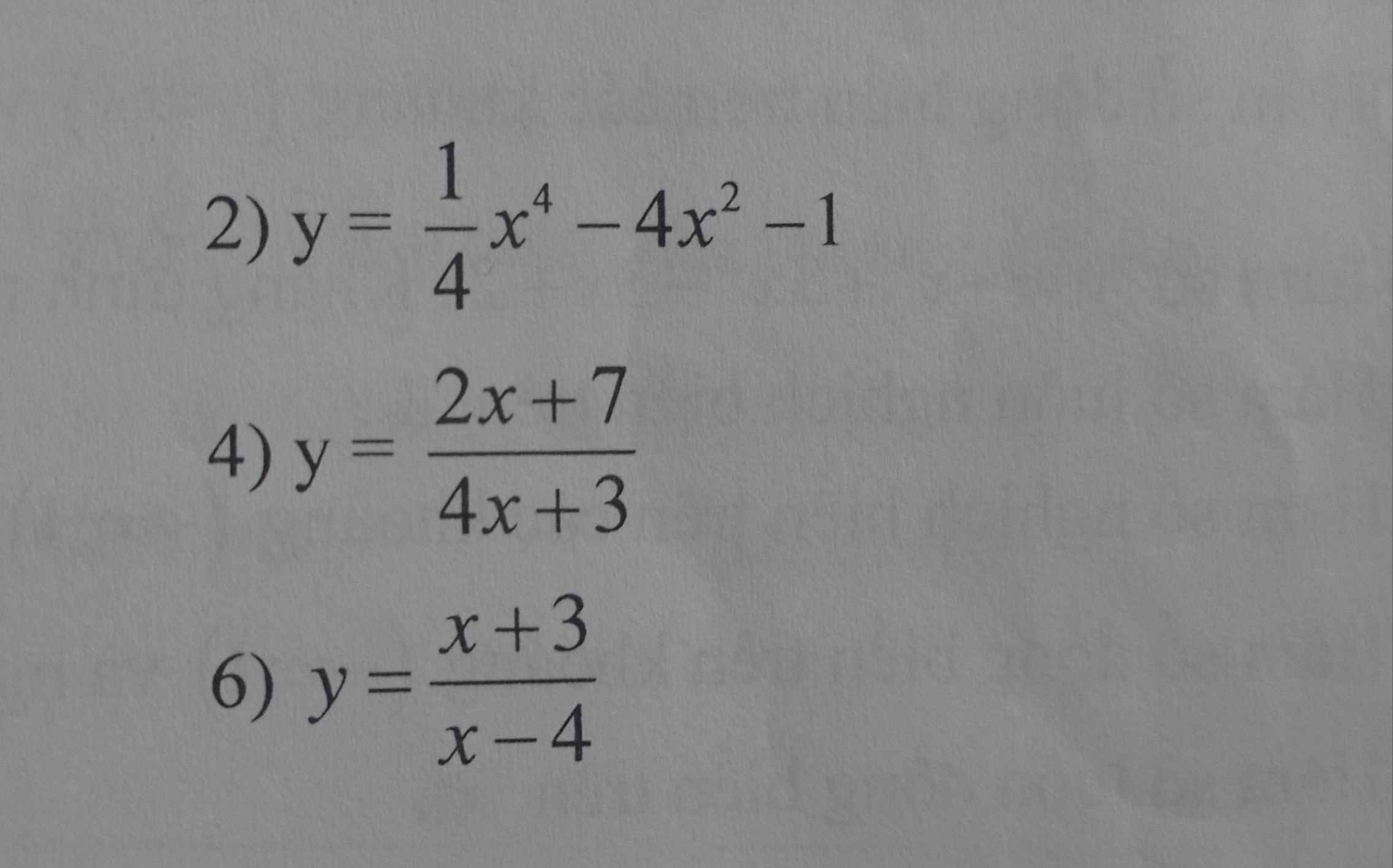

Những câu hỏi liên quan
Nêu cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm. Tìm các cực trị của hàm số: y = x 4 - 2 x 2 + 2
a)Cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm:
Quy tắc 1:
1. Tìm tập xác định.
2. Tính f'(x). Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.
3. Lập bảng biến thiên.
4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
1. Tìm tập xác định.
2. Tính f'(x). Giải phương trình f'(x) = 0 và kí hiệu xi (i = 1, 2, 3, ...) là các nghiệm của nó.
3. Tính f"(x) và f"(xi)
4. Nếu f"(xi) > 0 thì xi là điểm cực tiểu.
Nếu f"(xi) < 0 thì xi là điểm cực đại.
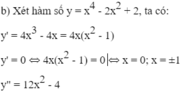
Dựa vào Quy tắc 2, ta có:
y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại.
y"(-1) = y"(1) = 8 > 0 ⇒ x = ±1 là hai điểm cực tiểu.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của m để hàm số
y
1
3
x
3
-
m
x
2
+
m
+
2
x
có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương. A.
m
∈
2...
Đọc tiếp
Tìm tất cả các giá trị của m để hàm số y = 1 3 x 3 - m x 2 + m + 2 x có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương.
A. m ∈ 2 - 2 7 3 ; - 1 ∪ 2 ; 2 + 2 7 3
B. m ∈ 2 - 2 7 3 ; 2 + 2 7 3
C. m ∈ - 1 ; 2
D. m ∈ - ∞ ; - 1 ∪ 2 ; + ∞
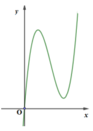

Để đồ thị hàm số có 2 điểm cực trị thì
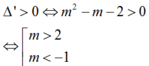
Khi đó, do a = 1 3 > 0 nên hàm số y = 1 3 x 3 - m x 2 + m + 2 x có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương . Đồ thị hàm số cắt trục hoành tại 1 điểm duy nhất là x = 0 1 và hai cực trị x 1 ; x 2 x 1 < x 1 thỏa mãn: 0 < x 1 < x 2 2
Ta có:
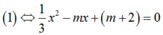
hoặc là vô nghiệm hoặc là có nghiệm kép x = 0
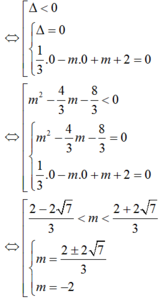
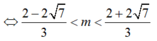
Kết hợp điều kiện ta có:
m ∈ 2 - 2 7 3 ; - 1 ∪ 2 ; 2 + 2 7 3
Chọn: A
Đúng 0
Bình luận (0)
Tìm các điểm cực trị và các giá trị cực trị của hàm số \(y = \sqrt{2x-x^3}\)
ĐKXĐ: \(2x-x^3>=0\)
=>\(x^3-2x< =0\)
=>\(\left[{}\begin{matrix}x< =-\sqrt{2}\\0< =x< =\sqrt{2}\end{matrix}\right.\)
\(y=\sqrt{2x-x^3}\)
=>\(y'=\dfrac{\left(2x-x^3\right)'}{2\cdot\sqrt{2x-x^3}}=\dfrac{2-3x^2}{2\cdot\sqrt{2x-x^3}}\)
Đặt y'=0
=>\(2-3x^2=0\)
=>\(3x^2=2\)
=>\(x^2=\dfrac{2}{3}\)
=>\(\left[{}\begin{matrix}x=\dfrac{\sqrt{6}}{3}\left(nhận\right)\\x=-\dfrac{\sqrt{6}}{3}\left(loại\right)\end{matrix}\right.\)
Khi \(x=\dfrac{\sqrt{6}}{3}\) thì \(y=\sqrt{2\cdot\dfrac{\sqrt{6}}{3}-\left(\dfrac{\sqrt{6}}{3}\right)^3}\)
\(=\sqrt{\dfrac{4\sqrt{6}}{9}}=\dfrac{2}{3}\cdot\sqrt{\sqrt{6}}\)
Đúng 2
Bình luận (1)
Cho hàm số
y
x
4
-
2
(
1
-
m
2
)
x
2
+
m
+
1
. Tìm tất cả các giá trị của tham số m để hàm số có...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( 1 - m 2 ) x 2 + m + 1 . Tìm tất cả các giá trị của tham số m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất
A. m = 0
B. m = - 1 2
C. m = 1
D. m = 1 2
Đáp án A
Phương pháp giải:
Tìm tọa độ điểm cực trị của đồ thị hàm số trùng phương và tính diện tích tam giác
Lời giải: TXĐ : D = R
Ta có ![]() R
R
Phương trình 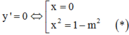
Hàm số có 3 điểm cực trị ó (*) có 2 nghiệm phân biệt khác ![]()
Khi đó 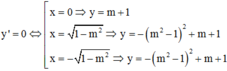
Gọi ![]() ;
; ![]() là ba điểm cực trị. Tam giác ABC cân tại A.
là ba điểm cực trị. Tam giác ABC cân tại A.
Trung điểm H của BC là ![]()
![]()
Và ![]()
Diện tích tam giác ABC là ![]()
![]()
Mà ![]() R suy ra
R suy ra ![]()
Vậy Smax = 1 Dấu bằng xảy ra khi và chỉ khi m = 0
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
-
2
(
1
-
m
2
)
x
2
+
m
+
1
. Tìm tất cả các giá trị của tham số thực m để hàm...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( 1 - m 2 ) x 2 + m + 1 . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất
A. m = - 1 2
B. m = 1 2
C. m = 0
D. m = 1
Chọn C
[Phương pháp tự luận]
![]()

Hàm số có cực đại , cực tiểu khi và chỉ khi m < 1
Tọa độ điểm cực trị A ( 0 ; m + 1 )
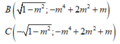
![]()
Phương trình đường thẳng BC: y + m 4 - 2 m 2 - m = 0
![]()
![]()
![]()
Vậy S đạt giá trị lớn nhất ⇔ m = 0
[Phương pháp trắc nghiệm]
![]()
![]()
![]()
![]()
Vậy S đạt giá trị lớn nhất ⇔ m = 0
Đúng 0
Bình luận (0)
Nêu cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm. Tìm các cực trị của hàm số \(y = x^4 – 2x^2 + 2\)
Xét hàm số : y = x4 – 2x2 + 2
Có đạo hàm là: y’ = 4x3 – 4x = 0 ⇔ x = 0, x = 1, x = -1
Đạo hàm cấp hai: y’’ = 12x2 – 4
y’’(0) = -4 < 0 ⇒ điểm cực đại xCD =0
y’’(-1) = 8 > 0, y’’(-1) = 8 > 0
⇒ các điểm cực tiểu xCT = -1, xCT = 1
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
(
m
-
1
)
x
+
2
có cực đại, cực tiểu và các đ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + ( m - 1 ) x + 2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. m ≥ 0
D. m > 1
Chọn D
Ta có y ' = 3 x 2 - 6 m x + m - 1
Hàm số có cực đại, cực tiểu khi và chỉ khi PT y ' = 0 có hai nghiệm phân biệt
Điều này tương đương
![]()
Hai điểm cực trị có hoành độ dương
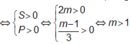
Vậy các giá trị cần tìm của m là m >1
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
-
2
m
x
2
+
m
2
-
2
. Tìm m để hàm số có 3 điểm cực trị và các điểm cực trị của đồ thị hàm số là ba đỉnh của một tam giác vuông? A. m 1 B. m ...
Đọc tiếp
Cho hàm số y = x 4 - 2 m x 2 + m 2 - 2 . Tìm m để hàm số có 3 điểm cực trị và các điểm cực trị của đồ thị hàm số là ba đỉnh của một tam giác vuông?
A. m = 1
B. m = - 1
C. m = 2
D. m = - 2
Tìm tất cả các giá trị thực của tham số m để hàm số
y
-
x
3
+
3
x
2
+
3
m
2
-
1
x
-
3
m
2
-
1
có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O. A.
m
±
1
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = - x 3 + 3 x 2 + 3 m 2 - 1 x - 3 m 2 - 1 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.
A. m = ± 1 2
B. m = 1 2
C. m = -1
D. m = ± 1
Chọn A
![]()
![]()
![]() là tam thức bậc hai có ∆' = m2.
là tam thức bậc hai có ∆' = m2.
Do đó: y có cực đại cực tiểu ⇔ y’ có hai nghiệm phân biệt
⇔ g(x) có hai nghiệm phân biệt ⇔ ∆' > 0 ⇔ m ≠ 0. (1)
Khi đó, y’ có các nghiệm là: 1 ± m
→ tọa độ các điểm cực trị của đồ thị hàm số là
![]()
![]()
![]()
![]()
![]()
Để A và B cách đều gốc tọa độ khi và chỉ khi :
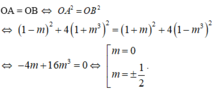
Đối chiếu với điều kiện (1), ta thấy chỉ m = ± 1 2 thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
-
2
1
-
m
2
x
2
+
m
+
1
. Tìm tất các giá trị của tham số m để hàm số cực đại, cực tiểu và các điểm cực trị của đồ thị lập thành một tam giác có diện tích lớn nhất A. ...
Đọc tiếp
Cho hàm số y = x 4 - 2 1 - m 2 x 2 + m + 1 . Tìm tất các giá trị của tham số m để hàm số cực đại, cực tiểu và các điểm cực trị của đồ thị lập thành một tam giác có diện tích lớn nhất
A. 1 2
B. 0
C. 1
D. - 1 2