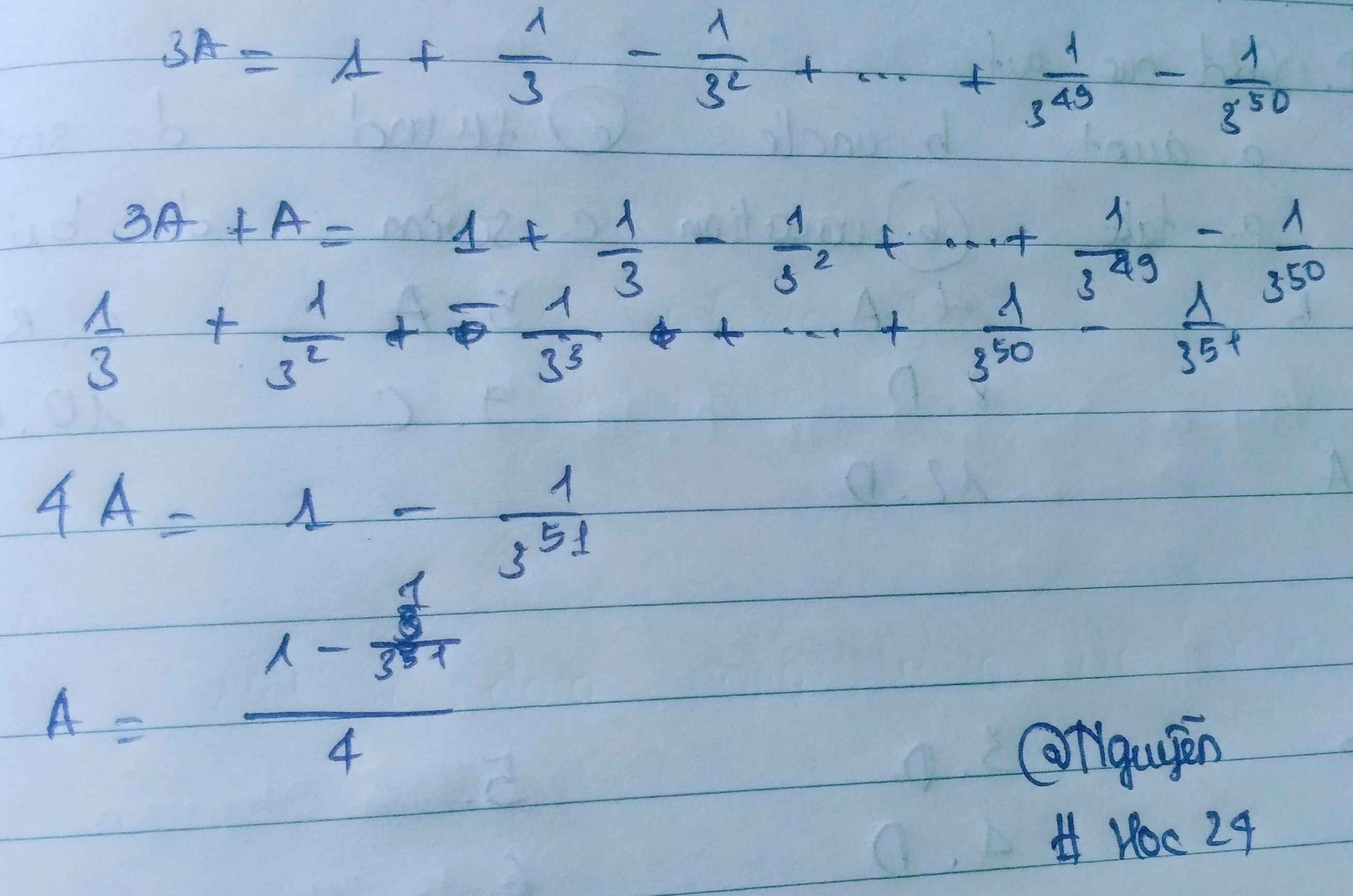B = -1/3 + 1/3^2 - 1/3^3 +...+ 1/3^50 - 1/3^51

Những câu hỏi liên quan
Tính
A=1+3^1-3^2+3^3-3^4+...........+3^99-3^100
B=50.(51^99+51^98+51^97+......+51^1+1)+1
Tính B = -1/3 + 1/3^2 - 1/3^3 + ....+ 1/3^50 - 1/3^51
B=-1/3+1/3^2-.....-1/3^51
3B=-1/3^2+1/3^3-.....-1/3^52
3B-B=(-1/3^2+1/3^3-....-1/3^52)-(-1/3+1/3^2-....-1/3^51)
2B= -1/3^52-1/3
2B= -1/3^52-3^51/3^52
2B= -1-3^51/3^52
B= -3^51-1/3^52x2
Đúng 0
Bình luận (0)
TÍNH B= -1/3+1/3^2-1/3^3+.....+1/3^50-1/3^51
B = -1/3 + 1/3^2 - 1/3^3 +...+ 1/3^50 - 1/3^51
tính B
tính \(B=\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{50}}-\dfrac{1}{3^{51}}\)
\(B=\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{50}}-\dfrac{1}{3^{51}}\)
\(=\dfrac{1}{\left(-3\right)}+\dfrac{1}{\left(-3\right)^2}+\dfrac{1}{\left(-3\right)^3}+...+\dfrac{1}{\left(-3\right)^{50}}+\dfrac{1}{\left(-3\right)^{51}}-\dfrac{1}{3}\)
\(=\dfrac{1}{\left(3\right)^2}+\dfrac{1}{\left(3\right)^3}+...+\dfrac{1}{\left(-3\right)^{51}}+\dfrac{1}{\left(-3\right)^{52}}\)
\(\Rightarrow\dfrac{4}{3}B=\dfrac{1}{-3}-\dfrac{1}{\left(-3\right)^{52}}=\dfrac{-3^{51}-1}{3^{52}}\Rightarrow B=\dfrac{-3^{51}-1}{4.3^{51}}\)
Đúng 4
Bình luận (0)
Giúp mình giải câu này với Tính B= -1/3+1/3^2-1/3^3+1/3^4-1/3^5+...+1/3^50-1/3^51
\(B=-\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+....+\dfrac{1}{3^{50}}-\dfrac{1}{3^{51}}\)
=> \(3B=-1+\dfrac{1}{3}-\dfrac{1}{3^2}+...+\dfrac{1}{3^{49}}-\dfrac{1}{3^{50}}\)
=> \(4B=-1-\dfrac{1}{3^{51}}\)
=> \(B=\dfrac{-1-\dfrac{1}{3^{51}}}{4}\)
Đúng 1
Bình luận (0)
BÀI 4 TÍNH NHANH
A,1+3+5+7+......+50 +51
B,1-2+3-4+5-.....-50+51
A. Số lượng số hạng là:
\(\left(51-1\right):2+1=26\) (số hạng)
Tổng: \(\left(51+1\right)\times26:2=676\)
B. \(1-2+3-4+5-...+51\)
\(=1+\left(-2+3\right)+\left(-4+5\right)+...+\left(-50+51\right)\)
\(=1+1+1+...+1\)
Số lượng số hạng (không tính số 1 đầu tiên) là:
\(\left(51-2\right):1+1=50\) (số hạng)
Số lượng cặp là: \(50:2=25\) (cặp)
Tổng là: \(1+25\times1=26\)
Đúng 2
Bình luận (0)
-1/3+1/3^2-1/3^3+...+1/3^50-1/3^51
TÍNH :B=-1/3+1/32-1/33+...+1/350-1/351