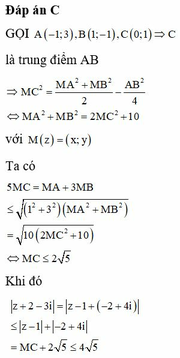Tìm số phức z thoả (2+i)^2 (1-i)z = 4 -3i +(3+i) z

Những câu hỏi liên quan
Cho N là điểm biểu diễn số phức z thỏa mãn \(\dfrac{z+2-3i}{z-3}=1-i\) và M là điểm biểu diễn số phức z' thoả mãn \(\left|z'-2-i\right|+\left|z'+3-3i\right|=\sqrt{29}\). Tìm giá trị nhỏ nhất của MN
Cho số phức z thoả mãn 2|z-1-i|=|z+2-3i|+2|z-4+i|. Giá trị lớn nhất của |z| bằng
A. 17
B. 13
C. 10
D. 2 5
Cho số phức z thoả mãn |z – 1 + 3i| + |z + 2 – i| = 8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của P = |2z + 1 = 2i|.
A. 8 và 4
![]()
![]()
![]()
Chọn D.
Ta có P = |2z + 1 = 2i| nên 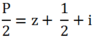
Ta cần tìm giá trị lớn nhất, giá trị nhỏ nhất của: 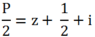
Ta có z1 = 1 - 3i; z2 = -2 + i và z0 = -1/2 - i
Ta thấy: ![]()
Tính 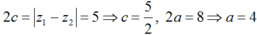
Suy ra 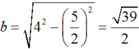
Vậy Max P = 2.4 = 8 và 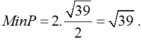
Đúng 0
Bình luận (0)
Cho hai số phức z,w thoả mãn |z-1-i|=1,| w ¯ -2-3i|=2. Giá trị nhỏ nhất của |z-w| bằng
A. 13 -3.
B. 17 -3.
C. 17 +3.
D. 13 +3
Cho số phức z thỏa mãn
5
z
-
i
z
+
1
-
3
i
+
3
z
-
1
+
i
.
Tìm giá trị lớn nhất M của
z
-
2...
Đọc tiếp
Cho số phức z thỏa mãn 5 z - i = z + 1 - 3 i + 3 z - 1 + i . Tìm giá trị lớn nhất M của z - 2 + 3 i ?
A. M = 10 3
B. M = 1 + 3
C. M = 4 5
D. M = 9
Cho số phức z thỏa mãn
5
z
-
i
z
+
1
-
3
i
+
3
z
-
1...
Đọc tiếp
Cho số phức z thỏa mãn 5 z - i = z + 1 - 3 i + 3 z - 1 + i .
Tìm giá trị lớn nhất M của z - 2 + 3 i
A. M= 10 3
B. M= 1 + 3
C. M= 4 5
D. M= 9
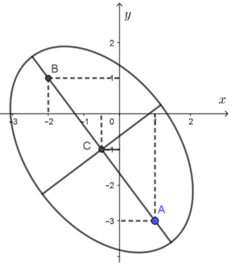
Đáp án C
Gọi ![]() là trung điểm AB
là trung điểm AB
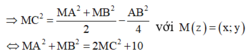
Ta có
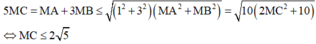
Khi đó
![]()
Đúng 0
Bình luận (0)
Cho số phức z thoả mãn |z-2+3i|=Căn5 và biểu thức P=|z+i|^2-|z-2|^2 đạt giá trị lớn nhất . Tính |z^2/3+4i|
Đặt \(z=x+yi\Rightarrow\) quỹ tích z là các điểm M thuộc đường tròn \(\left(x-2\right)^2+\left(y+3\right)^2=5\) có tâm \(I\left(2;-3\right)\) bán kính \(R=\sqrt{5}\)
\(P=x^2+\left(y+1\right)^2-\left(x-2\right)^2-y^2=4x+2y-3\)
\(P=4\left(x-2\right)+2\left(y+3\right)-1\le\sqrt{\left(4^2+2^2\right)\left[\left(x-2\right)^2+\left(y+3\right)^2\right]}-1=11\)
\(\Rightarrow P_{max}=11\) khi \(\frac{x-2}{4}=\frac{y+3}{2}\Rightarrow x=2y+8\)
Thay vào \(\left(x-2\right)^2+\left(y+3\right)^2=5\) tìm được \(x;y\Rightarrow\) tìm được \(z\)
Đúng 0
Bình luận (0)
Tìm số phức z thỏa mãn (1 + i)z + (2 - 3i)(1 + 2i) 7 + 3i. A. B. C. D.
Đọc tiếp
Tìm số phức z thỏa mãn (1 + i)z + (2 - 3i)(1 + 2i) = 7 + 3i.
A. ![]()
B. ![]()
C. ![]()
D. 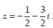
Chọn B.
Ta có: (2 - 3i).(1 + 2i) = 2 + 4i - 3i - 6i2 = 8 + i
Từ giả thiết : (1 + i)z + (2 - 3i)(1 + 2i) = 7 + 3i nên
(1 + i)z + (8 + i) = 7 + 3i hay (1 + i)z = -1 + 2i

Đúng 0
Bình luận (0)
Cho số phức z, biết
(
2
z
-
1
)
(
1
+
i
)
+
(
z
¯
+
1
)
(...
Đọc tiếp
Cho số phức z, biết ( 2 z - 1 ) ( 1 + i ) + ( z ¯ + 1 ) ( 1 - i ) = 2 - 2 i .
Tìm số phức liên hợp của số phức w=3z-3i
A. 1 3 - 1 3 i
B. 1 3 + 1 3 i
C. 1 - 4 i
D. 1 + 4 i
Chọn D.
Giả sử z=a+bi với a,b ∈ ℝ
Thay vào biểu thức ta được:
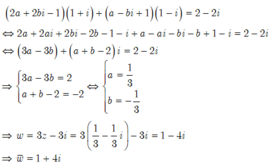
Đúng 0
Bình luận (0)