Cho A(1,2)B(3,0) tìm M để AMB là góc vuông

Những câu hỏi liên quan
cho hình vuông ABCD gọi M là một điểm trên BC N là một điểm trên CD sao cho góc AMB=AMN qua A kẻ AH vuông góc với MN
â) tam giác AMH=AMB
b) góc MAN =45do
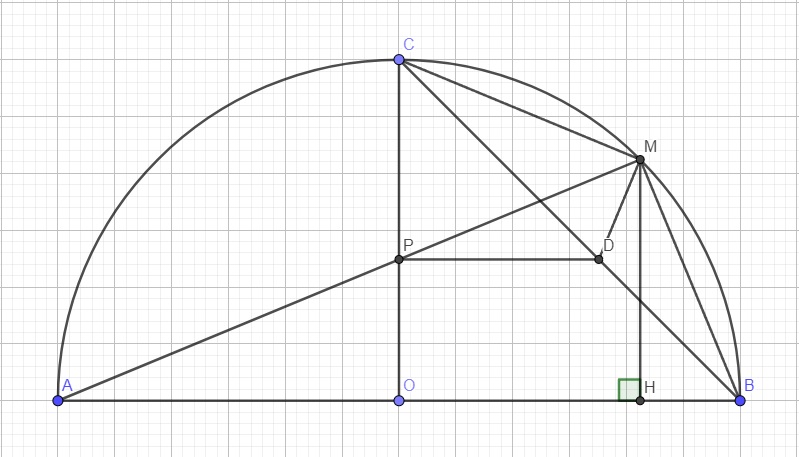
Cho nửa(O), đường kính AB =2R. vẽ bán kính OC vuông góc với AB. M là 1 điểm chuyển động trên cung BC nhỏ, AM cắt OC tại P
a) Tìm vị trí điểm M để PO=PM. Tính diện tích AMB theo R
b) Tìm vị trí điểm M để MB=MP. Tính diện tích AMB theo R
c) Gọi I là tâm đường tròn ngoại tiếp tam giác CPM. Khi M chuyển động I chạy trên đường nào ?
a.
AB là đường kính nên \(\widehat{AMB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{AMB}=90^0\)
\(\Rightarrow M\) và O cùng nhìn BP dưới 1 góc vuông nên tứ giác OBMP nội tiếp
Mà \(PO=PM\Rightarrow\widehat{PBO}=\widehat{PBM}\)
\(\Rightarrow\Delta_VPBO=\Delta_VPBM\left(ch-gn\right)\) (có cạnh huyền PB chung)
\(\Rightarrow BM=OB=R\)
Vậy M nằm ở vị trí sao cho \(BM=R\) thì \(PO=PM\)
Áp dụng Pitago: \(AM=\sqrt{AB^2-BM^2}=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
\(\Rightarrow S_{ABM}=\dfrac{1}{2}AM.BM=\dfrac{R^2\sqrt{3}}{2}\)
b.
\(MB=MP\Rightarrow\Delta MBP\) vuông cân tại M
\(\Rightarrow\widehat{BPM}=45^0\)
Theo câu a ta có OBMP nội tiếp \(\Rightarrow\widehat{BOM}=\widehat{BPM}=45^0\) (cùng chắn BM)
\(\Rightarrow\widehat{BOM}=\dfrac{1}{2}\widehat{BOC}\) \(\Rightarrow M\) là điểm chính giữa cung BC
Khi đó kẻ \(MH\perp AB\Rightarrow\Delta MOH\) vuông cân tại H (tam giác cân có góc đáy bằng 45 độ)
\(\Rightarrow MH=\dfrac{OM}{\sqrt{2}}=\dfrac{R\sqrt{2}}{2}\)
\(S_{AMB}=\dfrac{1}{2}MH.AB=R^2\sqrt{2}\)
c.
Qua P kẻ đường thẳng song song AB cắt BC tại D
\(\Rightarrow DP\perp CP\Rightarrow\Delta CPD\) nội tiếp đường tròn đường kính CD (1)
\(\widehat{MPD}=\widehat{MAB}\) (đồng vị), mà \(\widehat{MAB}=\widehat{MCB}\) (cùng chắn BM)
\(\Rightarrow\widehat{MPD}=\widehat{MCB}\)
\(\Rightarrow\) Tứ giác MCPD nội tiếp (2 góc bằng nhau cùng chắn MD) (2)
(1);(2) \(\Rightarrow\) M,C,P cùng thuộc đường tròn đường kính CD
Hay tâm I của tam giác CPM nằm trên đường thẳng BC khi M di động trên cung BC
Đúng 2
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn tâm O. M là một điểm thuộc cung AC(ko chứa B) kẻ MH vuông góc với AC;MK vuông góc với BC
a)CM: góc AMB=HMK
b)CM tam giác AMB đồng dạng với tam giác HMK
Cho 2 điểm A và B cố định và điểm M di động sao cho tam giác có 3 góc nhọn . Gọi H là trực tâm của rtam giác ABM và K là chân đường vuông góc vẽ từ M của tam giác AMB . Tìm GTLN của tích KH.KM
cho tam giác vuông vuông tại a có góc c = 30 độ . gọi m là trung điểm của bc , trên tia đối của tia MA lấy điểm d sao cho MD = MA .
a ) CM : △AMB = △DMC
b) CM : △ABC = △CDA
c) CM : △AMB là tam giác đều
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\hat{AMB}=\hat{DMC}\) (hai góc đối đỉnh)
MB=MC
Do đó: ΔAMB=ΔDMC
b: ΔAMB=ΔDMC
=>\(\hat{MAB}=\hat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC
Ta có: AB//DC
AB⊥CA
Do đó: CD⊥CA
ΔAMB=ΔDMC
=>AB=DC
Xét ΔBAC vuông tại A và ΔDCA vuông tại C có
BA=DC
AC chung
Do đó: ΔBAC=ΔDCA
c: ΔABC vuông tại A
=>\(\hat{ABC}+\hat{ACB}=90^0\)
=>\(\hat{ABC}=90^0-30^0=60^0\)
ΔBAC=ΔDCA
=>BC=DA
mà \(BM=CM=\frac{BC}{2};AM=MD=\frac{AD}{2}\)
nên BM=CM=AM=MD
Xét ΔMAB có MA=MB và \(\hat{ABM}=60^0\)
nên ΔMAB đều
Đúng 0
Bình luận (0)
Cho đường tròn o , điểm M nằm ngoài đường tròn . kẻ các tiếp tuyến MA,MB với đường tròn (B,C là các tiếp điểm) a,Chứng minh ∆AMB cân b,Cho góc AMB=60°.Tính gócAOB c,Chứng minh MO vuông góc AB
a: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>ΔMAB cân tại M
b: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}+\widehat{AMB}+\widehat{AOB}=360^0\)
=>\(\widehat{AOB}+60^0+90^0+90^0=360^0\)
=>\(\widehat{AOB}+240^0=360^0\)
=>\(\widehat{AOB}=120^0\)
c: ta có: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB
Đúng 1
Bình luận (0)
Cho hình vuông ABCD, M thuộc BC, qua M vẽ đường thẳng cắt DC ở K và góc AMB góc AMK. Từ A kẻ AH vuông góc MKa, cm: tam giác AMK tam giác AMBb, cm: góc KAM góc 45°Bài2Hình thang abcd, góc A góc D90°. CD2AB2AD. H là hình chiếu của D lên AC. M,P,Q lần lượt là trung điểm của CD,HC,HDa, cm: tứ giác ABMD vuông, tam giác BDC vuông cânb, cm: DMPQ là hình bình hànhc, cm AQ vuông góc DP
Đọc tiếp
Cho hình vuông ABCD, M thuộc BC, qua M vẽ đường thẳng cắt DC ở K và góc AMB= góc AMK. Từ A kẻ AH vuông góc MK
a, cm: tam giác AMK = tam giác AMB
b, cm: góc KAM= góc 45°
Bài2
Hình thang abcd, góc A= góc D=90°. CD=2AB=2AD. H là hình chiếu của D lên AC. M,P,Q lần lượt là trung điểm của CD,HC,HD
a, cm: tứ giác ABMD vuông, tam giác BDC vuông cân
b, cm: DMPQ là hình bình hành
c, cm AQ vuông góc DP
Cho các điểm A(2; 3), B(9; 4), M(5; y) và P(x; 2).
a, Tìm y để tam giác AMB vuông tại M;
b, Tìm x để ba điểm A, B và P thẳng hàng.
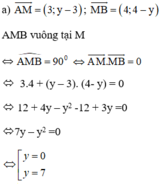
Vậy với M(5; 7) hoặc M(5; 0) thì tam giác ABM vuông tại M.

Vậy P(-5; 2)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại B có AC=2AB.Tia phân giác của góc A cắt BC tại M qua M kẻ đường vuông góc với AC tại H
a,Chứng minh góc AMB=góc AMH
b,Cứng minh tam giác AMB=tam giac AMH
c, Chứng minh AM=MC
d, Tính góc A,góc B của tam giác ABC
a: Ta có: \(\hat{AMB}+\hat{BAM}=90^0\) (ΔBAM vuông tại B)
\(\hat{HMA}+\hat{HAM}=90^0\) (ΔHAM vuông tại H)
mà \(\hat{BAM}=\hat{HAM}\)
nên \(\hat{BMA}=\hat{HMA}\)
b: Xét ΔABM vuông tại B và ΔAHM vuông tại H có
AM chung
\(\hat{BAM}=\hat{HAM}\)
Do đó: ΔABM=ΔAHM
c: ΔABM=ΔAHM
=>AB=AH
mà AC=2AB
nên AC=2AH
=>H là trung điểm của AC
Xét ΔMAC có
MH là đường cao
MH là đường trung tuyến
Do đó: ΔMAC cân tại M
=>MA=MC
c: ΔMAC cân tại M
=>\(\hat{MCA}=\hat{MAC}\)
=>\(\hat{MCA}=\frac12\cdot\hat{BAC}\)
ΔABC vuông tại B
=>\(\hat{BAC}+\hat{BCA}=90^0\)
=>\(\hat{BAC}+\frac12\cdot\hat{BAC}=90^0\)
=>\(\frac32\cdot\hat{BAC}=90^0\)
=>\(\hat{BAC}=90^0:\frac32=60^0\)
=>\(\hat{ACB}=60^0\cdot\frac12=30^0\)
Đúng 0
Bình luận (0)