giải phương trình : x2-2(m-2)x+2m-5=0(giải bằng Δ thường)
Bài 2: Cho phương trình x2- 2(m+2)x – 2m - 5 = 0 (1) a) Giải phương trình (1) khi m=2 b) Tìm m để phương trình (1) có hai nghiệm phân biệt x1, X2 thoả mãn: |x1-x2| = 2
a: Khi m=2 thì pt sẽ là \(x^2-8x-9=0\)
=>x=9 hoặc x=-1
b: \(\text{Δ}=\left(2m+4\right)^2-4\left(-2m-5\right)\)
\(=4m^2+16m+16+8m+20=4m^2+24m+36\)
\(=4\left(m^2+6m+9\right)=4\left(m+3\right)^2>=0\)
Để phương trình có hai nghiệm phân biệt thì m+3<>0
hay m<>-3
Theo đề, ta có: \(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=2\)
\(\Leftrightarrow\sqrt{\left(2m+4\right)^2-4\left(-2m-5\right)}=2\)
\(\Leftrightarrow\sqrt{4m^2+16m+16+8m+20}=2\)
\(\Leftrightarrow4m^2+24m+36=4\)
\(\Leftrightarrow m^2+6m+9=1\)
=>m+3=1 hoặc m+3=-1
=>m=-2 hoặc m=-4
Đối với mỗi phương trình sau, kí hiệu x1 và x2 là hai nghiệm (nếu có). Không giải phương trình, hãy điền vào những chỗ trống (...):
a ) 2 x 2 – 17 x + 1 = 0 ; Δ = … ; x 1 + x 2 = … ; x 1 . x 2 = … ; b ) 5 x 2 – x – 35 = 0 ; Δ = … ; x 1 + x 2 = … ; x 1 . x 2 = … ; c ) 8 x 2 – x + 1 = 0 ; Δ = … ; x 1 + x 2 = … ; x 1 . x 2 = … ; d ) 25 x 2 + 10 x + 1 = 0 ; Δ = … ; x 1 + x 2 = … ; x 1 . x 2 = … ;
a) 2 x 2 – 17 x + 1 = 0
Có a = 2; b = -17; c = 1
Δ = b 2 – 4 a c = ( - 17 ) 2 – 4 . 2 . 1 = 281 > 0 .
Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 17 / 2 x 1 x 2 = c / a = 1 / 2
b) 5 x 2 – x – 35 = 0
Có a = 5 ; b = -1 ; c = -35 ;
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 5 . ( - 35 ) = 701 > 0
Theo hệ thức Vi-et, phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 1 / 5 x 1 ⋅ x 2 = c / a = − 35 / 5 = − 7
c) 8 x 2 – x + 1 = 0
Có a = 8 ; b = -1 ; c = 1
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 8 . 1 = - 31 < 0
Phương trình vô nghiệm nên không tồn tại x1 ; x2.
d) 25 x 2 + 10 x + 1 = 0
Có a = 25 ; b = 10 ; c = 1
Δ = b 2 – 4 a c = 10 2 – 4 . 25 . 1 = 0
Khi đó theo hệ thức Vi-et có:
x 1 + x 2 = − b / a = − 10 / 25 = − 2 / 5 x 1 x 2 = c / a = 1 / 25
Giải phương trình 5 x 2 + 4 x – 1 = 0 bằng cách điền vào những chỗ trống:
a = …; b’ = …; c = …;
Δ’ = …; √(Δ') = ….
Nghiệm của phương trình:
x 1 = … ; x 2 = … .
a = 5; b’ = 2; c = -1;
Δ ’ = ( b ' ) 2 - a c = 2 2 - 5 . ( - 1 ) = 9 ; √(Δ') = 3
Nghiệm của phương trình:
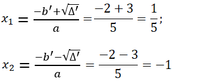
Giải phương trình 5x2 + 4x – 1 = 0 bằng cách điền vào những chỗ trống:
a = …; b’ = …; c = …;
Δ’ = …; √(Δ') = ….
Nghiệm của phương trình:
x1 = …; x2 = ….
a = 5; b’ = 2; c = -1;
Δ’ = (b')2 - ac = 22 - 5.(-1) = 9; √(Δ') = 3
Nghiệm của phương trình:
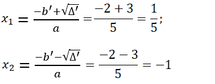
Câu 3. Cho phương trinh x ^ 2 - (2m - 1) * x - 8m = 0(1) ( m là tam số) a) Giải phương trình khi m=1 b) Tim m dễ phương trình có hai nghiệm phân biệt X1, X2 thoả mãn 3x1^2 + 3x2^2 + 2x₁X² = - 5
a: Khi m=1 thì (1) sẽ là:
x^2-x-8=0
=>\(x=\dfrac{1\pm\sqrt{33}}{2}\)
b: 3x1^2+3x2^2+2x1x2=5
=>3[(x1+x2)^2-2x1x2]+2x1x2=5
=>3[(2m-1)^2-2(-8m)]+2(-8m)=5
=>3(4m^2-4m+1+16m)-16m=5
=>12m^2+36m+3-16m-5=0
=>12m^2+20m-2=0
=>\(m=\dfrac{-5\pm\sqrt{31}}{6}\)
Cho phương trình x2 +(m-3)x-2m+2=0: Tìm giá trị của m để:
a) Phương trình có 2 nghiệm x1,x2 thỏa 2x1+x2=3
b)Phương trình có 2 nghiệm x1,x2 thỏa /x1-x2/=2
giải hộ mình với ạ mình sắp đi học rùiii
Cho phương trình x2 -2(m+1)x +m2+2m-3=0(m là than số)
a. giải phương trình khi m=0
b. Chứng tỏ phương trình luôn có 2 nghiệm phân biệt
a, Thay m = 0 vào phương trình trên ta được
\(x^2-2x-3=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\Leftrightarrow x=-1;x=3\)
Vậy với m = 0 thì x = -1 ; x = 3
Giải sử phương trình -x^2+(6-m)x-2m+3=0 có hai nghiệm x1, x2. Tính x1+x2+x1x2 theo m.
giải chi tiết cho phương trình: x2 - 2(m-1)x+2m-3=0 tìm tất cả các giá trị của m để phương trình có 2 nghiệm x1,x2 thỏa mãn x1 +m=2x2+1