Đặt \(A=5\cdot7^{2\left(n+1\right)}+2^{3n}=5\cdot49^{n+1}+8^n=5\left(41+8\right)^{n+1}+8^n\)

Áp dụng công thức nhị thức Newton, ta có:

\(\left(41+8\right)^{n+1}=41^{n+1}+\left(n+1\right)\cdot41^n\cdot8+\dfrac{n\left(n+1\right)}{2}\cdot41^{n-1}\cdot8^2+...+\left(n+1\right)\cdot41\cdot8^n+8^{n+1}\)

Vậy \(A=5\left[41^{n+1}+\left(n+1\right)\cdot41^n\cdot8+..+\left(n+1\right)\cdot41\cdot8^n+8^{n+1}\right]+8^n\)

\(\Rightarrow A=5\left[41^{n+1}\left(n+1\right)\cdot41^n\cdot8+...+\left(n+1\right)\cdot41\cdot8^n\right]+5\cdot8^{n+1}+8^n\)

Đặt \(B=41^{n+1}\left(n+1\right)\cdot41^n\cdot8+...+\left(n+1\right)\cdot41\cdot8^n\)

\(\Rightarrow B⋮41\)

Đặt \(C=5\cdot8^{n+1}+8^n=8^n\left(5\cdot8+1\right)=8^n\cdot41\)

\(\Rightarrow C⋮41\)

Mà \(A=B+C\Rightarrow A⋮41\)

\(\RightarrowĐPCM\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

góc B chung

=>ΔABC đồng dạng với ΔHBA

b: Xét ΔABC vuông tại A và ΔHAC vuông tại H có

góc C chung

=>ΔABC đồng dạng với ΔHAC

c: ΔABC đồng dạng với ΔHBA

ΔABC đồng dạng với ΔHAC

=>ΔHBA đồng dạng với ΔHAC

d: ΔABC đồng dạng với ΔHBA

=>BA/BH=BC/BA

=>BA^2=BH*BC

ΔABC đồng dạng với ΔHAC

=>CA/CH=CB/CA

=>CA^2=CH*CB

- Chắc là gọi thầy Nguyễn Việt Lâm thôi :)

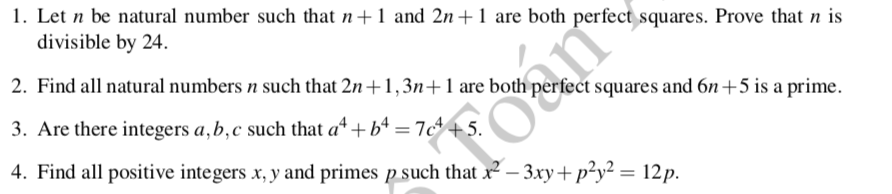
1.

\(2n+1\) luôn lẻ \(\Rightarrow2n+1=\left(2a+1\right)^2=4a^2+4a+1\Rightarrow n=2a\left(a+1\right)\)

\(\Rightarrow n\) chẵn \(\Rightarrow n+1\) lẻ \(\Rightarrow\) là số chính phương lẻ

\(\Rightarrow n+1=\left(2b+1\right)^2=4b^2+4b+1\)

\(\Rightarrow n=4b\left(b+1\right)\)

Mà \(b\left(b+1\right)\) là tích 2 số tự nhiên liên tiếp \(\Rightarrow\) luôn chẵn

\(\Rightarrow4b\left(b+1\right)⋮8\Rightarrow n⋮8\)

Mặt khác số chính phương chia 3 chỉ có các số dư 0 và 1

Mà \(\left(n+1\right)+\left(2n+1\right)=3n+2\) chia 3 dư 2

\(\Rightarrow n+1\) và \(2n+1\) đều chia 3 dư 1

\(\Rightarrow n⋮3\)

\(\Rightarrow n⋮24\) do 3 và 8 nguyên tố cùng nhau

2.

Lý luận tương tự bài 1, ta được n chẵn

Mặt khác các số chính phương chia 5 chỉ có các số dư 0, 1, 4

Mà: \(\left(2n+1\right)+\left(3n+1\right)=5n+2\) chia 5 dư 2

\(\Rightarrow2n+1\) và \(3n+1\) đều chia 5 dư 1

\(\Rightarrow2n⋮5\Rightarrow n⋮5\) (do 2 và 5 nguyên tố cùng nhau)

\(\Rightarrow n=5k\Rightarrow6n+5=5\left(6k+1\right)\)

- TH1: \(k=0\Rightarrow n=0\Rightarrow6n+5\) là SNT (thỏa mãn)

- TH2: \(k>0\Rightarrow6k+1>0\Rightarrow6n+5\) có 2 ước dương lớn hơn 1 \(\Rightarrow\) không là SNT (loại)

Vậy \(n=0\) là giá trị duy nhất thỏa mãn yêu cầu

a: Xét ΔCAE có

CD là đường cao

CD là trung tuyến

CD=AE/2

Do đó:ΔCAE vuông cân tại C

b: Xét ΔHAB có HI/HA=HK/HE

nên IK//AE và IK=1/2AE

=>IK=AD=BC

Xét tứ giác BIKC có

IK//BC

IK=BC

Do đó: BIKC là hình bình hành

Bạn tham khảo bài này nhé

Câu hỏi của be hat tieu - Toán lớp 7 - Học toán với OnlineMath

Chứng minh phân số tối giản hay phân số thập phân vậy ạ ?

10 chia 9luôn dư 1 10^n cung luôn dư 1 khi chia9

1+8=9 chia 9 dư 0 đpcm
vậy 10^

​