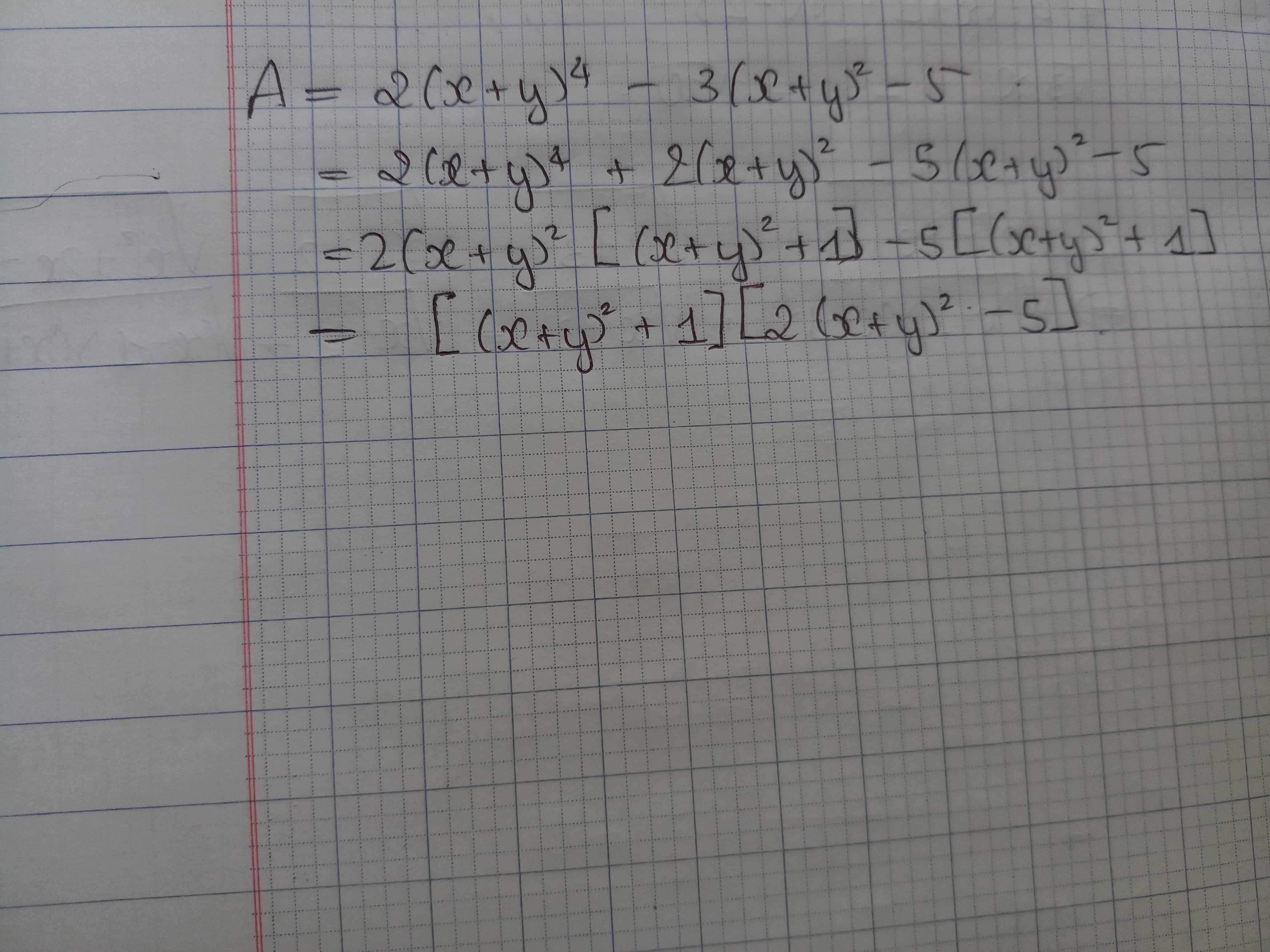Bài 1 :

\(x^2-6x+8=x^2-2x-4x+8=x\left(x-2\right)-4\left(x-2\right)=\left(x-4\right)\left(x-2\right)\)

Bài 2 :

 \(x^8+x^7+1=x^8+x^7+x^6+x^5+x^4+x^3+x^2+x+1-x^6-x^5-x^4-x^3-x^2-x\)

\(=x^6\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)+x^2+x+1-x^4\left(x^2+x+1\right)-x\left(x^2+x+1\right)\)

=\(\left(x^2+x+1\right)\left(x^6+x^3+1-x^4-x\right)\)

Tick đúng nha 

X^2-6+8

\(-8x^3+1=1^3-\left(2x\right)^3=\left(1-2x\right)\left(1+2x+4x^2\right)\)

khó dữ

a) X^2 -X -1 

= x- x^2 -1

= ( x - 1)^2

mk đang bận câu b tự làm nha

câu b nè dễ mà bn 

b)=6x^2-3x+2x-1

=3x(2x-1)+(2x-1)

=(3x-1)(2x-1)

Ta có: \(A=2\left(x+y\right)^4-3\left(x+y\right)^2-5\)

\(=2\left(x+y\right)^4-5\left(x+y\right)^2+2\left(x+y\right)^2-5\)

\(=\left(x+y\right)^2\left[2\left(x+y\right)^2-5\right]+\left[2\left(x+y\right)^2-5\right]\)

\(=\left[2\left(x+y\right)^2-5\right]\left[\left(x+y\right)^2+1\right]\)

x³ - 5x² + x - 5 = (x³ - 5x²) + (x - 5) = x²(x - 5) + (x - 5) = (x - 5)(x² + 1)

cho mk hỏi rút gọn bt nay nhé A=  1phần x+1  trừ x-1phân x cộng x+2 phần x^2 +x

\(=x^8+x^7-x^7+x^6-x^6+x^5-x^5+x^4-x^4+x^3-x^3+x^2-x^2+x+1\\ =x^6\left(x^2+x+1\right)-x^5\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)-x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)\\ =\left(x^2+x+1\right)\left(x^6-x^5+x^3-x^2+1\right)\)

đề sai rồi nhé

\(A=\left(x-1\right)\left(x-2\right)\left(x+7\right)\left(x+8\right)+8\)

\(A=\left[\left(x-1\right)\left(x+7\right)\right]\left[\left(x-2\right)\left(x+8\right)\right]+8\)

\(A=\left(x^2+6x-7\right)\left(x^2+6x-16\right)+8\)

Đặt \(q=x^2+6x-7\)ta có :

\(A=q\left(q-9\right)+8\)

\(A=q^2-9q+8\)

\(A=q^2-q-8q+8\)

\(A=q\left(q-1\right)-8\left(q-1\right)\)

\(A=\left(q-1\right)\left(q-8\right)\)

Thay \(q=x^2+6x-7\)vào A ta được :

\(A=\left(x^2+6x-7-1\right)\left(x^2+6x-7-8\right)\)

\(A=\left(x^2+6x-8\right)\left(x^2+6x-15\right)\)