(toán olympic lớp 3)
Cho tứ giác thường abcd có ab=4cm, cd =5cm, chu vi abcd = 25cm, tính tổng hai đường chéo tứ giác. bd + ac =?
Những câu hỏi liên quan
Cho tứ giác thường abcd có ab=4cm, cd =5cm, chu vi abcd = 25cm, tính tổng hai đường chéo tứ giác. bd + ac =?
(toán lớp 3 olimpic)
Cho tứ giác thường abcd có ab=4cm, cd =5cm, chu vi abcd = 25cm, tính tổng hai đường chéo tứ giác. bd + ac =?
2 đường chéo mà bạn, 16 là tổng 2 cạnh còn lại
Đúng 0
Bình luận (0)
1) Cho tứ giác ABCD có AC cắt BD tại O . Biết OA = 3cm, OB = 4cm , AB =5cm , OC =2OA ; OD=2OB .
Khi đó CD bằng: A.) 5cm. B.) 10cm . C.) 15cm . D.) 20cm .
2) Cho tứ giác ABCD . Hai đường chéo AC và BD cắt nhau tại O . Gọi E là điểm trong của tam giác OCD . Số tứ giác (tứ giác lồi và tứ giác không lồi) nhận 4 trong 5 điểm A, B , .., D , E làm đỉnh là:
A) 3
B) 6
C) 9
D) 12
1/ tính độ dài các canh a, B, c, d của một tứ giác có chu vi 76 và a:b:c:d 2:5:4:82/ CM nếu tứ giác ABCD có hai đường chéo AC vuông góc BD thì tổng các bình phương 2 cạnh đối này bằng tổng các bình phương hai cạnh đối kia,3/*bài này mình thực ra bik cách giải nhg lại ko bik trình bày nên nhờ các bạn giúp mình vớiĐường chéo BD của tứ giác ABCD chia tứ giác đó thành hai Δ ABD và CBD có chu vi lần lượt là 25cm và 27cm. Biết chu vi tứ giác là 32cm. Tính độ dài BD
Đọc tiếp
1/ tính độ dài các canh a, B, c, d của một tứ giác có chu vi =76 và a:b:c:d= 2:5:4:8
2/ CM nếu tứ giác ABCD có hai đường chéo AC vuông góc BD thì tổng các bình phương 2 cạnh đối này bằng tổng các bình phương hai cạnh đối kia,
3/*bài này mình thực ra bik cách giải nhg lại ko bik trình bày nên nhờ các bạn giúp mình với
Đường chéo BD của tứ giác ABCD chia tứ giác đó thành hai Δ ABD và CBD có chu vi lần lượt là 25cm và 27cm. Biết chu vi tứ giác là 32cm. Tính độ dài BD
Bài 3 mình làm được rồi, có phải bằng 10cm ko vậy ạ?
Đúng 0
Bình luận (0)
Tứ giác ABCD có các đường chéo cắt nhau tại O. Cho biết AC=4cm, BD = 5cm, A O B ^ = 60 0 . Tính diện tích tứ giác ABCD
Cho tứ giác ABCD có các đường chéo cắt nhau tại Ở . Cho biết AC=4cm,BD=5cm ,AOB=60° tính diện tích tứ giác ABCD
Lời giải:
Vận dụng bổ đề $S_{ABC}=\frac{1}{2}.AB.AC\sin A$ ta có:
$S_{ABCD}=S_{OAB}+S_{OBC}+S_{ODC}+S_{AOD}$
$=\frac{1}{2}.OA.OB.\sin \widehat{AOB}+\frac{1}{2}.OB.OC.\sin \widehat{BOC}+\frac{1}{2}.OD.OC.\sin \widehat{DOC}+\frac{1}{2}.OA.OD.\sin \widehat{AOD}$
$=\frac{1}{2}.OA.OB\sin 60^0+\frac{1}{2}.OB.OC.\sin 120^0+\frac{1}{2}.OD.OC\sin 60^0+\frac{1}{2}.OA.OD.\sin 120^0$
$=\frac{\sqrt{3}}{4}(OA.OB+OB.OC+OC.OD+OD.OA)$
$=\frac{\sqrt{3}}{4}(AC.BD)=\frac{\sqrt{3}}{4}.4.5=5\sqrt{3}$ (cm vuông)
Đúng 2
Bình luận (0)
Đường chéo AC của tứ giác ABCD chia tứ giác đó thành hai tam giác có chu vi 25cm và 27cm. Biết chu vi của tứ giác bằng 32cm đ. Tính độ dài AC
chu vi của tam giác abc là :
ab+bc+c=25 (1)
chu vi của tam giác acd là :
ac+cd+da=27 (2)
chu vi của tứ giác abcd là :
ab+cd+bc+da=32 (3)
từ (1) và(2) ta có :
ab+bc+ac+ac+cd+da=25+27=52 (4)
=>(ab+bc+cd+da)+2ac=52
từ (1)và(4) <=>32+2ac=52
=>2ac=52-32=20
=>ac=20:2=10
vậy ac=10cm
Đúng 0
Bình luận (0)
Tứ giác ABCD có AB = 4cm, BC = 20cm, CD = 25cm. DA = 8cm, đường chéo BD = 10cm.
a) Nếu cách vẽ tứ giác ABCD có kích thước đã cho ở trên.
b) Các tam giác ABD và BDC có đồng dạng với nhau không? Vì sao?
c) Chứng minh rằng AB // CD.
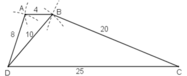
a) Cách vẽ:
- Vẽ ΔBDC:
+ Vẽ DC = 25cm
+ Vẽ cung tròn tâm D có bán kính = 10cm và cung tròn tâm C có bán kính = 20cm. Giao điểm của hai cung tròn là điểm B.
Nối DB và BC.
- Vẽ điểm A: Vẽ cung tròn tâm B có bán kính = 4cm và cung tròn tâm D có bán kính = 8cm. Giao điểm của hai cung tròn này là điểm A.
Nối DA và BA.
Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)
Cho tứ giác ABCDcos AB = 3cm, BC = 10cm, CD = 12cm, AD = 5cm và đường chéo BD = 6cm.
a) Chứng minh tam giác ABD đồng dạng với tam giác BDC
b) Chứng minh tứ giác ABCD là hình thang
c) Hai đường chéo AC và BD cắt nhau tại O. Tính DO