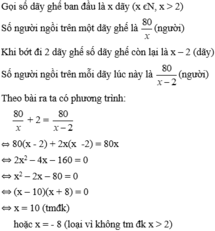
Vậy số dãy ghế ban đầu là 10 dãy và số người ngồi trên 1 dãy là 8 người.

Câu hỏi tương tự nha bạn

Gọi số dãy ghế ban đầu là a [a>0 ,a thuộc N]

=>Số người trên mỗi dãy ghế là : \(\frac{70}{a}\)

Khi bớt đi 2 dãy ghế => Số dãy ghế còn lại là : a-2

Số người trên mỗi dãy ghế lúc đó là : \(\frac{70}{a-2}\)

Theo bài ra ta có : \(\frac{70}{a}+4=\frac{70}{a-2}\)

=> 70[a-2]+4a[a-2]=70a =>35[a-2]+2a[a-2]=35a

=> 35a-70+2a\(^2\)-4a=35a

=> 2a\(^2\)-4a-70=0

=> \(a^2-2a-35=0=>a^2-2a+1-36=0=>\left[a-1^2\right]=36=6^2\). Có 2 trường hợp

Trường hợp 1 : a-1 = -6 => a = - 5 [loại]

Trường hợp 2 : a - 1 = 6 => a = 7

Còn đây bạn làm nốt tiếp

Vậy phòng họp lúc đầu có 7 dãy ghế và 10 người

Gọi x là số ghế lúc đầu \(\left(x\inℤ;x>2\right)\)

Ta có phương trình \(\frac{70}{x-2}-\frac{70}{x}=4\)

Giải phương trình được x = 7 ; x = -5

Chỉ có x = 7 thỏa mãn điều kiện đề bài

Vậy lúc đầu phòng họp có 7 dãy ghế và mỗi dãy có 10 người

Gọi x là số dãy ghế; y là số người trên mỗi dãy ghế (x,y>0) 
Ta có tổng cộng 80 người nên x*y =80 <=> x =80/y (1) 
Nếu bớt đi 2 dãy ghế tức x-2 thì mỗi dãy còn lại phải xếp thêm 2 người tức y+2 
Ta có: (x-2)*(y+2) = 80 (2) 
Thay (1) vào (2) ta có: 2y^2 +4y -160 =0 
<=> y=8 => x=10 
Vậy có 10 dãy ghế và có 8 người trên mỗi dãy

Gọi x là số dãy ghế trong phòng họp ( x nguyên ; x>2)

Số người ngồi trên 1 dãy là \(\frac{80}{x}\)(người)

Nếu bới đi 2 dãy thì số dãy ghế còn lại là : x - 2 (dãy)

Số người ngồi trên mỗi dãy sẽ là: \(\frac{80}{x-2}\)(người )

Ta có phương trình :

\(\frac{80}{x-2}-\frac{80}{x}=2\Leftrightarrow\frac{40}{x-2}-\frac{40}{x}=1\Leftrightarrow x^2-2x-80=0\)

Giaỉ phương trình ta được \(x_1=10;x_2=-8\left(lọai\right)\)

Vậy số dãy ghế lúc đầu là 10 dãy và mỗi dãy xếp 8 người ngồi

 Gọi số dãy là x, số người ngồi trong mỗi dãy là y dk:...
Theo bài ra ra có xy =70 (1)
Nếu ta bớt đi 2 dãy ghế thì mỗi dãy ghế còn lại phải xếp thêm 4 người ngồi mới đủ chỗ
=> (x-2)(y+4) = 70 (2)
Từ (1) và (2) ta có hệ phương trình...................
Giải ra được x = 7 ; y = 10

em học lớp 5 nên ko bt đâu ạ

Gọi số dãy lúc đầu là x

Theo đề, ta có: 70/(x-2)-70/x=4

=>(70x-70x+140)/(x^2-2x)=4

=>4x^2-8x-140=0

=>x=7

Gọi số dãy ghế lúc đầu là x(x \(\in\) N^* , x > 0)

Số ghế mỗi dãy: \(\dfrac{70}{x}\) (ghế)

Nếu bớt đi 2 dãy ghế ngồi thì mỗi dãy còn lại phải xếp thêm 4 người mới đủ chỗ ngồi.

\(\Rightarrow\left(x-2\right)\left(\dfrac{70}{x}+4\right)=70\) 

\(\Rightarrow4x-\dfrac{140}{x}+62=70\) 

\(\Rightarrow4x^2-140+62x=70x\) (do x \(\in\) N^* )

\(\Rightarrow4x^2-8x-140=0\) 

\(\Rightarrow x=-5\left(l\right);x=7\left(n\right)\)  

Vậy lúc đầu phòng họp có  dãy ghế.

Gọi số dãy ghế lúc ban đầu là x(dãy)

(Điều kiện: \(x\in Z^+\))

Số người ngồi trên 1 dãy ghế ban đầu là \(\dfrac{80}{x}\left(người\right)\)

Số dãy ghế khi bớt đi 2 dãy là x-2(dãy)

Số người ngồi trên 1 dãy ghế khi bớt đi 2 dãy ghế là \(\dfrac{80}{x-2}\left(người\right)\)

Theo đề, ta có phương trình:

\(\dfrac{80}{x-2}-\dfrac{80}{x}=2\)

=>\(\dfrac{80x-80\left(x-2\right)}{x\left(x-2\right)}=2\)

=>\(\dfrac{160}{x\left(x-2\right)}=2\)

=>x(x-2)=80

=>\(x^2-2x-80=0\)

=>(x-10)(x+8)=0

=>\(\left[{}\begin{matrix}x-10=0\\x+8=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=10\left(nhận\right)\\x=-8\left(loại\right)\end{matrix}\right.\)

Vậy: Số dãy ghế ban đầu là 10 dãy

Số người ngồi trên 1 dãy ban đầu là 80:10=8 người

bài mẫu nè:

gọi số dãy ghế là x, số ghê là y 
theo đb ta có hpt 
(x-2)(y+2)=288 
xy=288 
giải pt tìm đk x=18; y=16 

Gọi số dãy ghế ban đầu là a (a>0 và a thuộc N)

=> Số người trên mỗi dãy ghế là \(\frac{70}{a}\)

Khi bớt đi 2 dãy ghế => Số dãy ghế còn lại là: a-2

Số người trên mỗi dãy ghế lúc đó là: \(\frac{70}{a-2}\)

Theo bài ra ta có: \(\frac{70}{a}\)+4=\(\frac{70}{a-2}\)

<=> 70(a-2)+4a(a-2)=70a <=> 35(a-2)+2a(a-2)=35a

<=> 35a-70+2a²-4a=35a

<=> 2a²-4a-70=0

<=> a²-2a-35=0 <=> a²-2a+1-36=0 => (a-1)²=36=6². Có 2 TH:

+/ TH1: a-1=-6; => a=-5 (loại)

+/ TH2: a-1=6; => a=7

Vậy phòng họp lúc đầu có số dãy ghế là 7; mỗi ghế có 70:7=10 người ngồi

ĐS: 7 dãy ghế