cho ngũ giác ABCDE . Tính số đường thẳng vẽ được từ hai đỉnh của đa giác trên

Những câu hỏi liên quan
Cho ngũ giác ABCDE từ đỉnh của ngũ giác đã cho có thể lập được bao nhiêu vectơ có điểm cuối là A
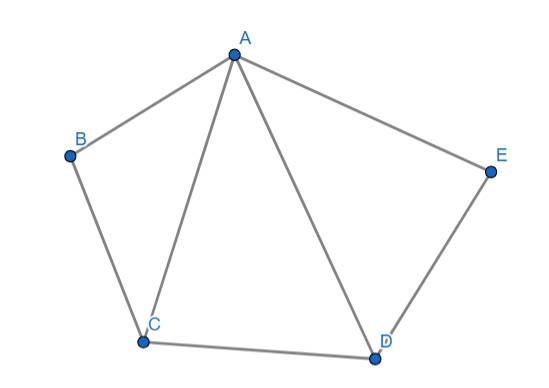
Ta có hình ngũ giác ABCDE ta có 4 cách lập vectơ có điểm cuối là điểm A
Các vectơ lập được là:
\(\overrightarrow{BA};\overrightarrow{CA};\overrightarrow{DA};\overrightarrow{EA}\)
Đúng 2
Bình luận (0)
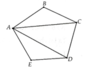
Cho ngũ giác ABCDE. Kẻ các đường chéo AC và AD. Kể tên các đa giác có trong hình vẽ.
Có 2 tam giác: ABC, ACD, ADE
Có 2 tứ giác: ABCD, ACDE
Có 1 ngũ giác: ABDE
Đúng 0
Bình luận (0)
Cho tứ giác ABCD,đoạn thẳng nối hai đỉnh ko kề nhau được gọi là đường chéo.Ví dụ :tứ giác ABCD có hai đường chéo là AC và BD.
a/Hỏi ngũ giác ABCD có những đường chéo nào ?
b/Hỏi đa giác ABCDEFMN có mấy đường chéo? Đa giác n cạnh
a: Các đường chéo của ABCDE là;
AD,BE,AC,BD
b: Số đường chéo của đa giác ABCDEFMN là;
\(C^2_8-8=20\left(đường\right)\)
Đúng 0
Bình luận (0)
Cho ngũ giác ABCDE. Có bao nhiêu vectơ được lập ra từ các cạnh và đường chéo của ngũ giác?
A. 5
B. 10
C. 15
D. 20
* Với điểm đầu là A: Có 4 vectơ được lập ra từ các cạnh và đường chéo của ngũ giác là: A B → ; A C → ; A D → ; A E →
* Tương tự với các đỉnh còn lại.
* Do đó, số vectơ được lập ra từ các cạnh và đường chéo của ngũ giác là 4.5 = 20 vecto
Đáp án D
Đúng 1
Bình luận (0)
a) Tính tổng các góc trong của đa giác 5 cạnh.
b) Cho ngũ giác đều ABCDE. Gọi F là giao điểm hai đường chéo AC và BE.
Chứng minh tứ giác CFED là hình thoi.
cj kham khảo
a) Nối AC; AD
Ngũ giác ABCDE được chia thành 3 tam giác: ΔABC, ΔACD, ΔADE. Tổng các góc trong của mỗi tam giác bằng 1800
Tổng các góc trong của ngũ giác ABCDE là 1800. 3 = 5400
b) Vì ABCDE là ngũ giác đều nên
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=\widehat{E}=\frac{540^0}{5}=108^0\)
Mặt khác ΔABC cân tại B nên
\(\widehat{BAC}+\widehat{BCA}=\frac{180^0-108^0}{2}=36^0\)
\(\Rightarrow\widehat{CAE}=\widehat{ACD}=108^0-36^0=72^0\)
\(\Rightarrow\widehat{EDC}+\widehat{ADC}=108^0+72^2=180^0\)
Suy ra ED // AC hay ED // CF.
Chứng minh tương tự ta có EF // CD
Mặt khác ED = DC (gt)
nên tứ giác CEFD là hình thoi.
Cho ngũ giác ABCDE.Gọi I là giao điểm của AD và BE
Chứng minh: D I 2 = AI.AD
Hướng dẫn: vẽ đường tròn ngoại tiếp ngũ giác đều ABCDE rồi xét hai tam giác đồng dạng AIE và AED
vẽ đường tròn ngoại tiếp ngũ giác đều ABCDE
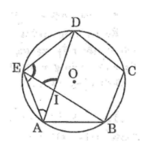

Suy ra tam giác DEI cân tại D ⇒ DI = DE
Mà DE =AE
Nên DI = AE (7)
Từ (4) và (7) suy ra: D I 2 = AI.AD
Đúng 0
Bình luận (0)
Cho ngũ giác đều ABCDE. Gọi I là giao điểm của AD và BE. Chứng minh \(DI^2=AI.AD\)
Hướng dẫn : Vẽ đường tròn ngoại tiếp ngũ giác đều ABCDE rồi xét hai tam giác đồng dạng AIE và AED
Cho ngũ giác ABCDE. Kẻ AH \(\perp\)CD, EN // AD, BM // AC ( M,N thuộc đường thẳng CD). Biết AH= h, MN= a. Tính diện tích ngũ giác ABCDE theo h,a.
Cho ngũ giác lồi. Mỗi cạnh và mỗi đường chéo của ngũ giác được tô bởi 1 trong 2 màu xanh hoặc đỏ sao cho không có 3 đoạn thẳng nào tạo thành 1 tam giác cùng màu
cmr từ mỗi đỉnh của ngũ giác xuất phát đúng 2 đoạn thẳng đỏ, 2 đoạn thẳng xanh

















