vẽ đường tròn ngoại tiếp ngũ giác đều ABCDE
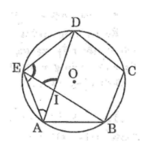

Suy ra tam giác DEI cân tại D ⇒ DI = DE
Mà DE =AE
Nên DI = AE (7)
Từ (4) và (7) suy ra: D I 2 = AI.AD
vẽ đường tròn ngoại tiếp ngũ giác đều ABCDE


Suy ra tam giác DEI cân tại D ⇒ DI = DE
Mà DE =AE
Nên DI = AE (7)
Từ (4) và (7) suy ra: D I 2 = AI.AD
1.Cho đường tròn (0) . Tam giác ABC nội tiếp đường tròn . Các đường cao CF , BE , AD , H là trực tâm của tam giác ABC . Gọi K là điểm đối xứng vs H qua BC . AA' là đường kính a, Chứng minh tứ giác ABKC nội tiếp b, chứng minh EF vuông góc với AO c, gọi I là trung điểm của BC . Chứng minh 3 điểm H , I , A' thẳng hàng d, Gọi G là trọng tâm của tam giác ABC . Chứng minh diện tích AGH = 2 diện tích AGO
2.Trong mặt phẳng tọa độ Oxy cho ngũ giác lồi ABCDE có tọa độ các đỉnh là các số nguyên. Chứng minh tồn tại ít nhất một điểm nằm trong ngũ giác đó có tọa độ là các số nguyên
Cho tam giác ABC vuông tại A ( AC > AB) có đường cao AH = 4,8cm và trung tuyến AM = 5 cm. Đường tròn tâm ( H;\(\frac{HA}{2}\)) giao AC tại E và giao tia tới của BA tại D
a) Chứng minh D,H,E thẳng hàng
b) Chứng minh tam giác ABC đồng dạng với tam giác AED. Tính tỷ số đồng dạng
c)Gọi I là tâm đường tròn ngoại tiếp tứ giác BECD. Tính diện tích tứ giác AHDM
Cho tam giác ABC vuông tại A ( AC > AB) có đường cao AH = 4,8cm và trung tuyến AM = 5 cm. Đường tròn tâm ( H;$\frac{HA}{2}$HA2 ) giao AC tại E và giao tia tới của BA tại D
a) Chứng minh D,H,E thẳng hàng
b) Chứng minh tam giác ABC đồng dạng với tam giác AED. Tính tỷ số đồng dạng
c)Gọi I là tâm đường tròn ngoại tiếp tứ giác BECD. Tính diện tích tứ giác AHDM
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Kẻ đường cao AH và đường kính AD. Gọi M và N lần lượt là hình chiếu vuông góc của B và C trên AD. Chứng minh rằng tam giác ABC đồng dạng với tam giác HMN và trung điểm I của cạnh BC cũng là tâm đường tròn ngoại tiếp tam giác HMN.
Cho tam giác ABC nhọn (AB<AC), kẻ phân giác AD của góc BAC và đường trung tuyến AM (M,D thuộc BC). Vẽ 2 đường tròn ngoại tiếp các tam giác ABC và ADM, 2 đường tròn này cắt nhau tại điểm thứ 2 là I, đường tròn ngoại tiếp tam giác ADM cắt 2 cạnh AB và AC theo thứ tự tại E và F. Tia AD cắt đường tròn ngoại tiếp tam giác ABC tại J.
a, Chứng minh 3 điểm I; M; J thẳng hàng.
b, Gọi K là trung điểm È, tia MK cắt AC và tia BA theo thứ tự tại P và Q. Chứng minh tam giác PAQ cân
Cho tam giác ABc , lấy D trên cạnh BC , vẽ đường tròn tâm I qua D tiếp xúc với AB tại B. Vẽ đường tròn tâm K qua D tiếp xúc với AC tại C . Gọi M là giao điểm của hai đường tròn đó
1. CM : tứ giác ABMC nội tiếp
2. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC . CM : 3 đường tròn tâm I, tâm K và tâm O đồng quy
3. CM : MD di chuyển qua 1 điểm cố định
Cho đường tròn (O; R) đường kính BC. Điểm A ở bên ngoài đường tròn với OA = 2R. Vẽ hai tiếp tuyến AD, AE với đường tròn (O; R) trong đó D, E là các tiếp điểm.
1. Chứng minh tứ giác ADOE nội tiếp và xác định tâm I của đường tròn ngoại tiếp tứ giác ADOE.
2. Chứng minh rằng tam giác ADE đều.
3. Vẽ DH vuông góc với CE với H thuộc CE . Gọi P là trung điểm của DH, CP cắt đường tròn (O) tại
điểm Q khác điểm C, AQ cắt đường tròn (O) tại điểm M khác điểm Q. Chứng minh: AQ . AM = 3R^2
4. Chứng minh đường thẳng AO là tiếp tuyến của đường tròn ngoại tiếp tam giác ADQ.
cho tam giác ABC ngoại tiếp đường tròn tâm i gọi D ,E ,F lần lượt là các tiếp điểm của các cạnh BC CA AB với đường tròn tâm i .gọi m là giao điểm của AB và BC, AD cắt đường tròn tâm i tại n .gọi k là giao điểm của AC và EF .a)Chứng minh rằng IKND là tứ giác nội tiếp .b) chứng minh rằng MN là tiếp tuyến của đường tròn tâm I.