a,Xét \(\Delta AHB\) và \(\Delta BCD\) có :

\(\widehat{H}=\widehat{C}=90^0\)

\(\widehat{ABH}=\widehat{BDC}\left(ABCD\cdot là\cdot HCN,slt\right)\)

\(\Rightarrow\Delta AHB\sim\Delta BCD\left(g-g\right)\)

b, Ta có : \(\Delta AHB\sim\Delta BCD\left(cmt\right)\)

\(\Rightarrow\dfrac{AH}{BC}=\dfrac{HB}{DC}\)

\(\Rightarrow\dfrac{AH}{HB}=\dfrac{BC}{DC}\left(1\right)\)

Ta có : EC là phân giác \(\widehat{BCD}\)

\(\Rightarrow\dfrac{EB}{ED}=\dfrac{BC}{CD}\left(2\right)\)

\(\left(1\right)\left(2\right)\Rightarrow\dfrac{AH}{HB}=\dfrac{EB}{ED}\)

\(\Rightarrow AH.ED=HB.EB\left(ĐPCM\right)\)

c, Xét ΔABD vuông tại A, định lý Pi-ta-go ta được :

\(\Rightarrow BD=\sqrt{AD^2+AB^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)

Xét \(\Delta HDA\) và \(\Delta ADB\) có  :

\(\widehat{A}=\widehat{AHB}=90^0\)

\(\widehat{D}:chung\)

\(\Rightarrow\Delta HDA\sim\Delta ADB\left(g-g\right)\)

\(\Rightarrow\dfrac{AH}{AB}=\dfrac{AD}{BD}\)

hay \(\dfrac{AH}{4}=\dfrac{3}{5}\)

\(\Rightarrow AH=\dfrac{4.3}{5}=2,4\left(cm\right)\)

Xét ΔAHD vuông tại H, định lí Pi-ta-go ta được :

\(\Rightarrow DH=\sqrt{3^2-2,4^2}=1,8\left(cm\right)\)

Ta có : EC là phân giác \(\widehat{BCD}\)

\(\Rightarrow\dfrac{EB}{ED}=\dfrac{BC}{DC}\)

hay \(\dfrac{EB}{ED}=\dfrac{3}{4}\)

\(\Rightarrow\dfrac{EB}{3}=\dfrac{ED}{4}=\dfrac{EB+ED}{3+4}=\dfrac{5}{7}\)

\(\Rightarrow EB=\dfrac{5}{7}.3=\dfrac{15}{7}\left(cm\right)\)

Ta có : \(EH=BD-DH-EB=5-1,8-\dfrac{15}{7}=\dfrac{37}{35}\) (cm)

\(\Rightarrow S_{AHE}=\dfrac{2,8.\dfrac{37}{35}}{2}=1,48\left(cm^2\right)\)

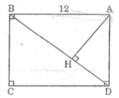
Vì  △ AHB đồng dạng △ BCD nên:

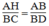
Suy ra: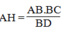 

Áp dụng định lí Pi-ta-go vào tam giác vuông BCD,ta có:

B D 2 = B C 2 + C D 2 = B C 2 + A B 2

= 12 2 + 9 2  = 225

Suy ra: BD = 15cm

Vậy AH = (12.9)/15 = 7,2 cm

mik cần câu c thôi

a: Áp dụng định lí Pytago vào ΔBDC vuông tại C, ta được:

hay DB=15(cm)

Xét ΔBDC có 

BE là đường phân giác ứng với cạnh DC

nên 

Lời giải:

Ta có:

$AB.AC=AH.BC=40$ 

$AB^2+AC^2=BC^2=100$

$\Rightarrow (AB+AC)^2=AB^2+AC^2+2AB.AC=180$

$\Rightarrow AB+AC=6\sqrt{5}$

Theo định lý Viet đảo, $AB,AC$ là nghiệm của pt $X^2-6\sqrt{5}X+40=0$

$\Rightarrow AB=4\sqrt{5}; AC=2\sqrt{5}$ (giả sử $AB>AC$)
Dễ thấy $AIHK$ là hình chữ nhật do có 3 góc vuông $\widehat{A}=\widehat{I}=\widehat{K}=90^0$

$\Rightarrow IK=AH=4$

Theo định lý Pitago: $AI^2+AK^2=IK^2=16(1)$

Mặt khác, theo hệ thức lượng trong tam giác vuông:

$AI.AB=AH^2$

$AK.AC=AH^2$

$\Rightarrow AI.AB=AK.AC\Rightarrow \frac{AI}{AK}=\frac{AC}{AB}=\frac{2\sqrt{5}}{4\sqrt{5}}=\frac{1}{2}(2)$

Từ $(1);(2)\Rightarrow AI=\frac{4\sqrt{5}}{5}; AK=\frac{8\sqrt{5}}{5}$ (cm)

Chu vi AIHK:

$P=2(AI+AK)=2(\frac{4\sqrt{5}}{5}+\frac{8\sqrt{5}}{5})=\frac{24\sqrt{5}}{5}$ (cm)

Diện tích AIHK:

$S=AI.AK=\frac{4\sqrt{5}}{5}.\frac{8\sqrt{5}}{5}=6,4$ (cm vuông)

Hình vẽ:

a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có

\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//CD)

Do đó: ΔAHB~ΔBCD

b: ta có: ΔABD vuông tại A

=>\(AB^2+AD^2=BD^2\)

=>\(BD^2=12^2+5^2=169\)

=>\(BD=\sqrt{169}=13\left(cm\right)\)

Xét ΔABD vuông tại A có AH là đường cao

nên \(AH\cdot BD=AB\cdot AD\)

=>\(AH\cdot13=12\cdot5=60\)

=>\(AH=\dfrac{60}{13}\left(cm\right)\)

c: Xét ΔBCD có CE là phân giác

nên \(\dfrac{EB}{ED}=\dfrac{BC}{CD}\)(1)

Xét ΔHAB vuông tại H và ΔADB vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔHAB~ΔADB

=>\(\dfrac{HA}{AD}=\dfrac{HB}{AB}\)

=>\(\dfrac{HA}{HB}=\dfrac{AD}{AB}=\dfrac{BC}{CD}\left(2\right)\)

Từ (1),(2) suy ra \(\dfrac{EB}{ED}=\dfrac{HA}{HB}\)

=>\(EB\cdot HB=HA\cdot ED\)