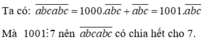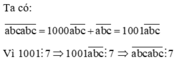abcabc chia hết cho 7 ; 11 ; 13

Những câu hỏi liên quan
a b c a b c ¯ có chia hết cho 7 không?
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích cấu tạo số. Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: a b c a b c ¯ = 1000. a b c ¯ + a b c ¯ = 1001. a b c ¯ Mà 1001 ⋮ 7 nên a b c a b c ¯ có chia hết cho 7. |
Đúng 0
Bình luận (0)
Vì sao aaaaaa chia hết cho 7? Vì sao abcabc chia hết cho 7,11 và 13?
ta có:abcabc=abc.1001=abc.7.11.13 chia hết cho 7,11 và 13
Đúng 0
Bình luận (0)
a) ab + ba chia hết cho 11
b) aaaaaa chia hết cho 7
c) abcabc chia hết cho 11
abcabc chia hết cho 7
abcabc chia hết cho 13 ( cùng chia hết cho 11;13;7)
GIÚP MIK VỚI CÁC BN ƠI !
a b c a b c ¯ chia hết cho 7 không, vì sao
Chứng minh rằng a b c a b c ¯ chia hết cho 7
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích số. Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: a b c a b c ¯ = 1000 a b c ¯ + a b c ¯ = 1001 a b c ¯ Vì 1001 ⋮ 7 ⇒ 1001 a b c ¯ ⋮ 7 ⇒ a b c a b c ¯ ⋮ 7 |
Đúng 0
Bình luận (0)
Chứng minh rằng a b c a b c ¯ chia hết cho 7
CMR \(\dfrac{ }{abcabc}\) chia hết cho 7, 11, 13
Ta có: \(\overline{abcabc}=\overline{abc}\times1001\)
Mà: \(1001=7\times11\times13\)
\(\Rightarrow\overline{abcabc}=\overline{abc}\times7\times13\times11\) ⋮ 7, 13, 11 (đpcm)
Đúng 0
Bình luận (0)
Chứng tỏ ( abcabc + ababab ) chia hết cho 7
abcabc = 100000a+10000b+1000c+100a+10b+c
ababab = 100000a+10000b+1000a+100b+10a+b
-->(abcabc +ababab ) =201110a+20111b+1001c
=91(2210a+221b+11c)
= 7.13 (2210a+221b+11c) chia hết cho 7
Đúng 0
Bình luận (0)
Giải:
Ta có:
abcabc = 100000.a + b.10000 + c.1000 + a.100 + b.10 +c
ababab = 100000.a + b.10000 + a.1000 + b.100 + a.10 + b
\(\Rightarrow\) abcabc + ababab = 201110.a + 20111.b + 1001.c = 91.( 2210.a + 221.b + 11.c ) chia hết cho 7 ( vì 91 = 13.7 chia hết cho 7 )
\(\Rightarrowđpcm\)
Đúng 0
Bình luận (0)
1) Chứng minh: ab+cd chia hết cho 11 thì abcd chia hết cho 11
2) Chứng minh abcabc chia hết cho 7
1) abcd = ab x 100 + cd
= ab x 99 + ab + cd
Vậy nếu ab + cd chia hết cho 11
Thì abcd chia hết cho 11
Đúng 0
Bình luận (0)
chứng minh rằng a) \(\overline{abcabc}\) chia hết cho 7, 11, 13
b) \(\overline{ab}-\overline{ba}\) chia hết cho 9
c) \(\overline{abc}-\overline{cba}\) chia hết cho 99
a) Ta có: \(\overline{abcabc}=100000a+10000b+1000c+100a+10b+c\) \(=100100a+10010b+1001c\) \(=1001\left(100a+10b+c\right)=7\cdot11\cdot13\left(100a+10b+c\right)⋮7,11,13\)
b) Ta có: \(\overline{ab}-\overline{ba}=10a+b-10b-a=9a-9b\) \(=9\left(a-b\right)⋮9\)
c) Ta có: \(\overline{abc}-\overline{cba}=100a+10b+c-100c-10b-a=99a-99c=99\left(a-c\right)⋮99\)
Đúng 2
Bình luận (0)