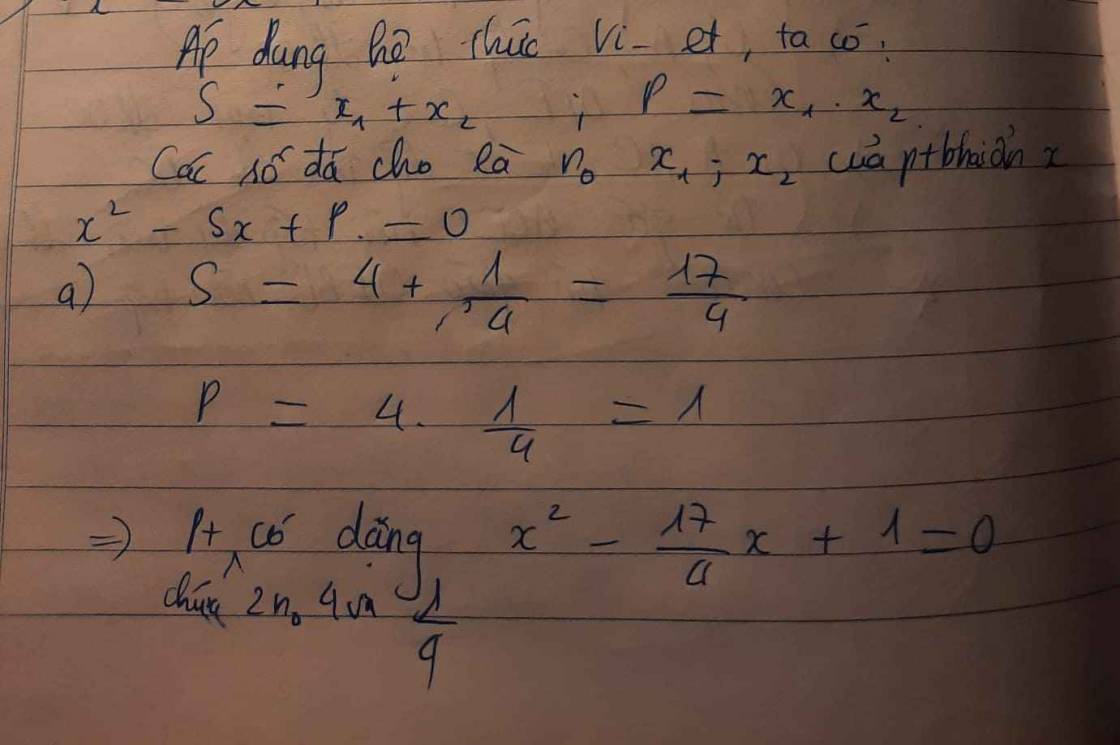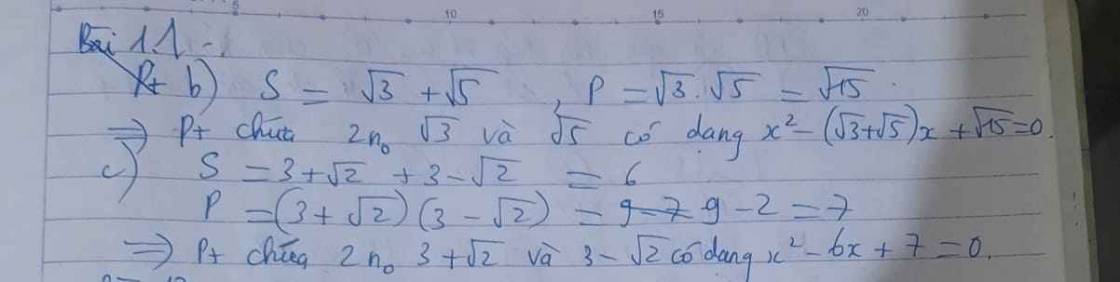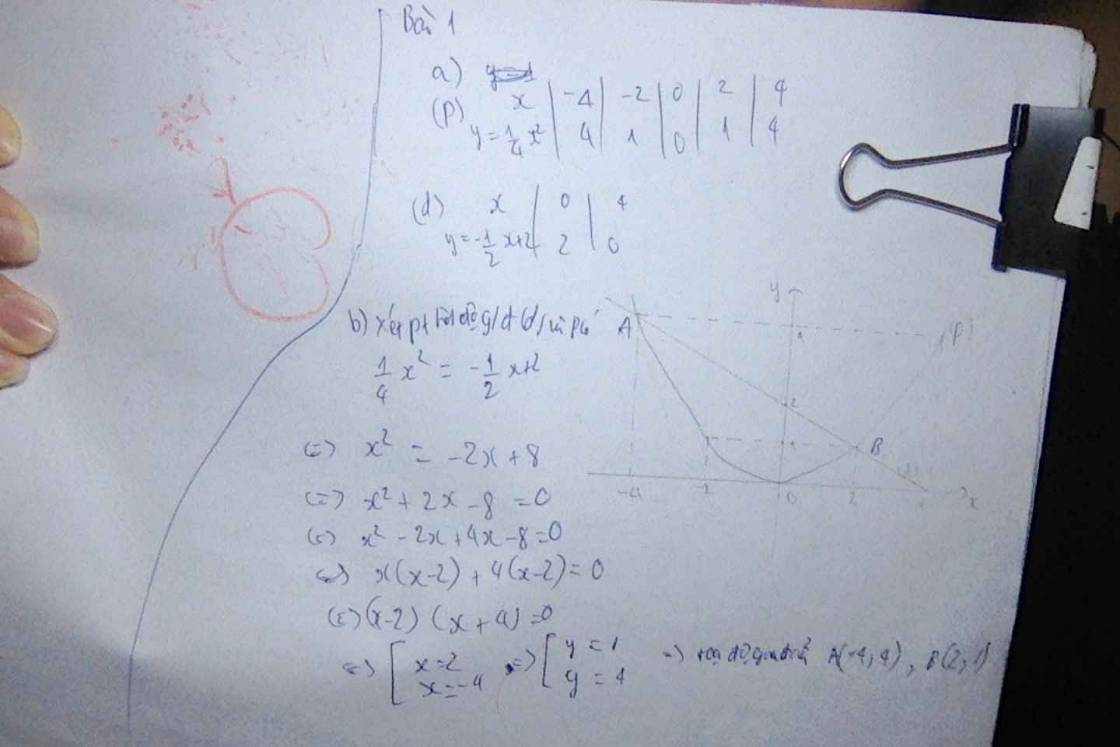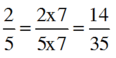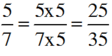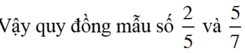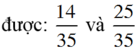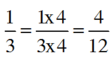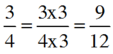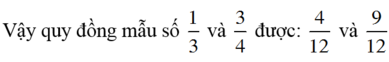\(quy đồng : \dfrac56 và \dfrac14\)

Những câu hỏi liên quan
\(\dfrac56 x (\dfrac12 + \dfrac12) \)
\(\dfrac{5}{6}\times\left(\dfrac{1}{2}+\dfrac{1}{2}\right)=\dfrac{5}{6}\times\dfrac{2}{2}=\dfrac{5}{6}\times1=\dfrac{5}{6}\)
Đúng 4
Bình luận (6)
Xem thêm câu trả lời
\(\dfrac12 + \dfrac14\)
\(\dfrac{1}{2}+\dfrac{1}{4}=\dfrac{2}{4}+\dfrac{1}{4}=\dfrac{3}{4}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Lập phương trình bậc hai có các nghiệm:
a) $4$ và $\dfrac14$;
b) $\sqrt{3}$ và $\sqrt{5}$;
c) $3+\sqrt{2}$ và $3-\sqrt{2}$.
a) x2 -\(\dfrac{17}{4}x+1=0\)
b) x2-(\(\sqrt{3}+\sqrt{5}\))x+\(\sqrt{15}=0\)
c)x2-6x+7=0
Xem thêm câu trả lời
Cho parabol $(P)$: $y = \dfrac14 x^2$ và đường thẳng $(d):$ $y = -\dfrac12x + 2$.
a. Vẽ $(P)$ và $(d)$ trên cùng hệ trục tọa độ.
b. Tìm tọa độ giao điểm của $(P)$ và $(d)$ bằng phép tính.
b,
Phương trình hoàng độ giao điểm của (p) và (d) là:
1
4
x
2
=
−
1
2
x
+
2
⇔
1
4
x
2
+
1
2
x
−
2
=
0
⇔
x
2
+
2
x
−
8
=
0
⇔
(
x
+
4
)
(
x
−
2
)
=
0
⇔
\orbr
{
x
=
−
4
x
=
2
x
=
−
4
⇒
y
=
4
x
=
2
⇒
y
=
1
Vậy tọa độ giao điểm của (p) và (d) là (-4;4) ; (2;1)
vậy tọa độ (P) và (d) là A (2;1) và B(-4;4)
Quy đồng các phân số
Quy đồng các phân số
7/9 và 2/5 b , 6/7 và 17/21
\(\dfrac{7}{9}=\dfrac{7\times5}{9\times5}=\dfrac{35}{45}\)
\(\dfrac{2}{5}=\dfrac{2\times9}{5\times9}=\dfrac{18}{45}\)
\(---------\)
\(\dfrac{6}{7}=\dfrac{6\times3}{7\times3}=\dfrac{18}{21}\)
\(\dfrac{17}{21}=\dfrac{17}{21}\)
Đúng 2
Bình luận (0)
không quy đồng mẫu số không quy đồng tử số
16/51 và 31/90
ơ bạn ơi không quy đòng mẫu số không quy đồng tử số thì làm sao so sánh được hả bạn, cái này là phân số chứ có phải số tự nhiên đâu
Đúng 0
Bình luận (0)
Quy đồng mẫu số các phân số (theo mẫu):Mẫu:
2
3
và
1
4
.
2
3
2
×
4
3
×
4
8
12
;
1
4
1...
Đọc tiếp
Quy đồng mẫu số các phân số (theo mẫu):
Mẫu: 2 3 và 1 4 .
2 3 = 2 × 4 3 × 4 = 8 12 ; 1 4 = 1 × 3 4 × 3 = 3 12 .
Vậy qua đồng mẫu số của 2 3 và 1 4 được 8 12 và 3 12 .
Quy đồng: 2 3 và 5 7
Quy đồng mẫu số các phân số (theo mẫu):Mẫu:
2
3
và
1
4
.
2
3
2
×
4
3
×
4
8
12
;
1
4
1...
Đọc tiếp
Quy đồng mẫu số các phân số (theo mẫu):
Mẫu: 2 3 và 1 4 .
2 3 = 2 × 4 3 × 4 = 8 12 ; 1 4 = 1 × 3 4 × 3 = 3 12 .
Vậy qua đồng mẫu số của 2 3 và 1 4 được 8 12 và 3 12 .
Quy đồng: 1 3 và 3 4
tìm 20 phân số ở giữa 2 phân số -1/3 và -1/7 mà không quy đồng mẫu và không quy đồng tử