mk giải câu a thui nha

để \(\frac{6n-1}{3n+2}\)là số nguyên thì:

    (6n-1) sẽ phải chia hết cho(3n+2)

mà (3n+2) chja hết cho (3n+2)

=> 2(3n+2) cx sẽ chia hết cho (3n+2)

<=> (6n+4) chia hết cho (3n+2)

mà (6n-1) chia hết cho (3n+2)

=> [(6n+4)-(6n-1)] chja hết cho (3n+2)

      (6n+4-6n+1) chja hết cho 3n+2

           5 chia hết cho3n+2

=> 3n+2 \(\in\){1,5,-1,-5}

ta có bảng

vậy....
 

bạn có thể giải thích ra được không !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

mình năm nay mới lên lớp 6

\(A = {6n-1\over 3n+2} \),A là số nguyên nên 6n-1 phải chia hết cho 3n+2. Suy ra 3n+2 là ước của 6n-1 =  \({\pm 1 , \pm (6n-1)}\)

.với 3n+2 =1 => n=\(x = {-1\ \ \over 3}\) (loại)

.Với 3n+2= -1=> n= -1 => A= 7 ( thỏa mãn )

.với 3n +2 =6n-1 => n = 1 => A = 1 (Thỏa mãn )

.với 3n+2 =1-6n => n=\(x = {-1 \ \over 9}\) (loại )

Kết luận vậy n = { -1,1 }

bài lớp 6 học sinh giỏi đấy

Đề nào vậy pạn? +vân?

mk biết nhưng mk ko chắc lắm!!!! xin lỗi nhé^^

Điều kiện xác định của phân thức: n ≠ 2

Ta có:

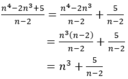
Vậy để N nguyên thì 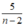 nguyên ⇒ n – 2 là ước của 5;  Ư ( 5 ) = - 1 ; 1 ; - 5 ; 5

n - 2= -1 ⇒ n =1;

n – 2 = 1 ⇒ n =3;

n – 2 = -5 ⇒ n = - 3;

n – 2 = 5 ⇒ n = 7;

vì n ∈ N nên n = 1; n = 3; n = 7

Vậy với n ∈ { 1; 3; 7} thì 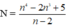 có giá trị là số nguyên

Để chia \(n^4-3n^3+n^2-3n+1\) cho \(n^2+1\) có giá trị nguyên

⇔ \(n^4-3n^3+n^2-3n+1\) \(⋮n^2+1\)

⇔ \(1⋮n^2+1\)

\(\Leftrightarrow n^2+1\inƯ\left(1\right)=\left\{1;-1\right\}\)

Lỡ có sai sót thì thông cảm giúp mình nha:3