Gọi 3 số tự nhiên liên tiếp lần lượt là a,a+1,a+2 (a \(\in\) N)

Có: a²+(a+1)²=(a+2)²

=>a²+a²+2a+1=a²+4a+4

=>a²+2a+1=4a+4

=>a²+1=2a+4

=>a²+1-2a-4=0

=>a²-2a-3=0

=>a²-3a+a-3=0

=>a(a-3)+(a-3)=0

=>(a+1)(a-3)=0

=>a=-1 hoặc a=3

Mà a \(\in\) N

=>a=3

Vậy STN nhỏ nhất là 3

Gọi 3 số đó là a ; a + 1 và a + 2

Có :

\(a^2+\left(a+1\right)^2=\left(a+2\right)^2\)

\(2a^2+2a+1=a^2+4+4a\)

\(\Rightarrow a^2=3+2a\)

\(a^2-2a-3=0\)

\(\left(a^2-3a\right)+\left(a-3\right)=0\)

\(\left(a-3\right)\left(a+1\right)=0\)

\(\Rightarrow\orbr{\begin{cases}a=3\\a=-1\end{cases}}\)

Mà a là số tự nhiên nên a = 3

Vậy ...

Gọi 3 số tnlt lần lượt là k,k+1,k+2

Theo bài ra ta có:

a²+(a+1)²=(a+2)²

=>2a²+2a+1=a²+4+4a=>a²=3+2a=>a²-3-2a=0

=>a²-3a+a-3=0=>(a²-3a)+(a-3)=0

=>(a-3)(a+1)=0

=>a-3=0 hoặc a+1=0

=>a=3 hoặc a=-1

Mà a là STN =>a=3

Vậy số cần tìm là 3

Gọi 3 số nguyên liên tiếp là a-1, a, a+1 (a ∈ Z)

Theo đề ta có \(\left(a-1\right)^2+a^2=\left(a+1\right)^2\)

\(\Leftrightarrow a^2-2a+1+a^2=a^2+2a+1\)

\(\Leftrightarrow a^2-4a=0\)

\(\Leftrightarrow a\left(a-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=0\\a=4\end{matrix}\right.\)

Vậy có 2 cặp 3 số nguyên liên tiếp đó là \(\left(-1;0;1\right)\) và \(\left(3;4;5\right)\)

Tick nha bạn 😘

Gọi 3 số tự nhiên liên tiếp đó là \(a;a+1;a+2\left(a\in N\right)\)

Theo đề bài ta có :

\(\left(a+2\right)^2-a\left(a+1\right)=79\)

\(\Leftrightarrow a^2+4a+4-a^2-a=79\)

\(\Leftrightarrow\left(a^2-a^2\right)+\left(4a-a\right)+4=79\)

\(\Leftrightarrow3a+4=79\)

\(\Rightarrow a=25\)

Vậy 3 số tự nhiên liên tiếp cần tìm là 25; 26; 27

Dễ thôi

Gọi ba số tự nhiên liên tiếp lần lượt là n;n+1;n+2

Tích cùa số đầu và số cuối là: \(n\left(n+2\right)=n^2+2n\)

Bình phương số giữa: \(\left(n+1\right)^2=n^2+2n+1\)

Dễ thấy hiệu hai giá trị trên là 1 => đpcm

Đáp án C

Gọi d = 2 x  là công sai

ta có bốn số là  a - 3 x , a - x , a + x , a + 3 x

Khi đó, từ giả thiết ta có:

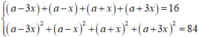
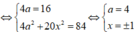
⇔ 1 , 3 , 5 , 7 7 , 5 , 3 , 1

Tổng bình phương của số hạng đầu và cuối là  1 2 + 7 2 = 50