Cho x2 + y2 + z2 + 2x - 4y + 6z = -14 . Tính x + y + z
Những câu hỏi liên quan
Trong không gian Oxyz, cho mặt phẳng (P): 2x - 2y + z + 1 0 và mặt cầu (S):
x
2
+
y
2
+
z
2
+ 2x + 4y - 6z + 10 0. Khẳng định nào dưới đây là đúng? A. (P) và (S) có vô số điểm chung B. (P) tiếp xúc với (S) C. (P) không cắt (S) D. Cả ba khẳng định trên đều sai
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P): 2x - 2y + z + 1 = 0 và mặt cầu (S): x 2 + y 2 + z 2 + 2x + 4y - 6z + 10 = 0. Khẳng định nào dưới đây là đúng?
A. (P) và (S) có vô số điểm chung
B. (P) tiếp xúc với (S)
C. (P) không cắt (S)
D. Cả ba khẳng định trên đều sai
Trong không gian với hệ tọa độ Oxyz, cho
(
a
)
:
2
x
−
2
y
−
z
+
14
0
, mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
−
2
x
−
4
y
−
6
z
−
11...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ( a ) : 2 x − 2 y − z + 14 = 0 , mặt cầu ( S ) : x 2 + y 2 + z 2 − 2 x − 4 y − 6 z − 11 = 0 . Mặt phẳng (P)//(a) cắt (S) theo thiết diện là một hình tròn có diện tích 16 π . Khi đó phương trình mặt phẳng (P) là:
A. 2 x − 2 y − z + 14 = 0
B. 2 x − 2 y − z + 4 = 0
C. 2 x − 2 y − z + 16 = 0
D. 2 x − 2 y − z − 4 = 0
Đáp án D.
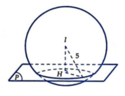
(P )//( α ) ⇒ ( P ) : 2 x − 2 y − z + c = 0 (c ≠ 14)
(S) có tâm I ( 1 ; 2 ; 3 ) , bán kính R=5
Hình tròn thiết diện (C) có S = 16 π =>Bán kính r = 4
Gọi H là hình chiếu của I lên (P) =>H là tâm của (C)
⇒ I H = d ( I ; ( P ) ) = R 2 − r 2 = 3
⇒ 2.1 − 2.2 − 3 + c 2 2 + 2 2 + 1 2 = 3 ⇔ c − 5 = 9 ⇔ c = 14 ( 1 ) c = − 4 ⇒ ( P ) : 2 x − 2 y − z − 4 = 0
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho
(
a
)
:
2
x
−
2
y
−
z
+
14
0
, mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
−
2
x
−
4
y
−
6
z
−
11...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ( a ) : 2 x − 2 y − z + 14 = 0 , mặt cầu ( S ) : x 2 + y 2 + z 2 − 2 x − 4 y − 6 z − 11 = 0 . Mặt phẳng (P)//(a) cắt (S) theo thiết diện là một hình tròn có diện tích 16 π . Khi đó phương trình mặt phẳng (P) là
A. 2 x − 2 y − z + 14 = 0
B. 2 x − 2 y − z + 4 = 0
C. 2 x − 2 y − z + 16 = 0
D. 2 x − 2 y − z − 4 = 0
4. Tìm giá trị lớn nhất của các biểu thức a. A = 5 – 8x – x2 b. B = 5 – x2 + 2x – 4y2 – 4y 5. a. Cho a2 + b2 + c2 = ab + bc + ca chứng minh rằng a = b = c b. Tìm a, b, c biết a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0 6. Chứng minh rằng: a. x2 + xy + y2 + 1 > 0 với mọi x, y b. x2 + 4y2 + z2 – 2x – 6z + 8y + 15 > 0 Với mọi x, y, z 7. Chứng minh rằng: x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
6
z
...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 - 2 x - 4 y - 6 z = 0 . Tính diện tích mặt cầu (S).
A. 42 π
B. 36 π
C. 9 π
D. 12 π
Đáp án B
Ta có:
=> (S) có bán kính R =3
Diện tích mặt cầu là: 4 π . 3 2 = 36 π
Đúng 0
Bình luận (0)
![Ckun []~(￣▽￣)~*[]~(￣▽...](https://hoc24.vn/images/avt/avt145702769_256by256.jpg)
1 tháng 4 2022 lúc 9:25
Chứng minh:
a. x2 + xy + y2 + 1 > 0 với mọi x, y
b. x2 + 4y2 + z2 - 2x - 6z + 8y + 15 > 0 Với mọi x, y, z
⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
x^2+4y^2+z^2-2x-6z+8y+15
=x^2+4y^2+z^2-2x-6z+8y+1+1+4+9
=(x^2-2x+1)+(4y^2+8y+4)+(z^2-6z+9)+1
=(x-1)^2+4(y+1)^2+(z-3^)2+1
Ta thấy:(x−1)^2≥0
4(y+1)^2≥0
(z−3)^ 2≥0
{(x−1)^24(y+1)^2(z−3)^2≥0
⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
⇒(x−1)2+4(y+1)2+(z−3)2+1≥0+1=1>0
Đúng 3
Bình luận (1)
\(x^2+xy+y^2+1.=x^2+2.x.\dfrac{y}{2}+\left(\dfrac{y}{2}\right)^2+\dfrac{3}{4}y^2+1.\\ =\left(x+\dfrac{y}{2}\right)^2+\dfrac{3}{4}y^2+1>0\forall x;y\in R.\\ \Rightarrow x^2+xy+y^2+10\forall x;y\in R.\)
Đúng 3
Bình luận (0)
Trong không gian với trục tạo độ Oxyz, cho mặt phẳng (
α
): 2x - 2y + z -3 0 và mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
+
4
y
-
6
z
+
9
0
. Khi đó, phát biểu nào sau đây đúng? A. (
α...
Đọc tiếp
Trong không gian với trục tạo độ Oxyz, cho mặt
phẳng ( α ): 2x - 2y + z -3 = 0 và mặt cầu
(S): x 2 + y 2 + z 2 - 2 x + 4 y - 6 z + 9 = 0 . Khi đó,
phát biểu nào sau đây đúng?
A. ( α ) không cắt (S)
B. ( α ) tiếp xúc với (S)
C. ( α ) cắt (S) theo giao tuyến là một đường tròn có bán kính nhỏ hơn bán kính của (S)
D. ( α ) cắt (S) theo giao tuyến là một đường tròn có tâm trùng với tâm của (S)
Đáp án C
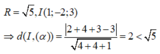
⇒ ( α ) cắt ( β ) theo giao tuyến là một đường tròn có bán kính nhỏ hơn bán kính của (S)
Đúng 0
Bình luận (0)
Trong không gian với trục tọa độ Oxy, cho mặt phẳng
(
α
)
:
2
x
−
2
y
+
z
−
3
0
và mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
−
2
x
+
4
y
−
6
z
+...
Đọc tiếp
Trong không gian với trục tọa độ Oxy, cho mặt phẳng ( α ) : 2 x − 2 y + z − 3 = 0 và mặt cầu ( S ) : x 2 + y 2 + z 2 − 2 x + 4 y − 6 z + 9 = 0 . Khi đó, phát biểu nào sau đây đúng?
A. ( α ) không cắt (S).
B. ( α ) tiếp xúc với (S).
C. ( α ) cắt theo giao tuyến là một đường tròn có bán kính nhỏ hơn bán kính của (S).
D. ( α ) cắt (S) theo giao tuyến là một đường tròn có tâm trùng với tâm của (S).
Trong không gian Oxyz cho mặt phẳng (P):2x-2y-z-40 và mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
6
z
-
11
0
. Biết rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn (C) là:
Đọc tiếp
Trong không gian Oxyz cho mặt phẳng (P):2x-2y-z-4=0 và mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 4 y - 6 z - 11 = 0 . Biết rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn (C) là:
Trong không gian Oxyz cho mặt phẳng
P
:
2
x
-
2
y
-
z
-
4
0
và mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
6
z
-
11...
Đọc tiếp
Trong không gian Oxyz cho mặt phẳng
P : 2 x - 2 y - z - 4 = 0 và mặt cầu
S : x 2 + y 2 + z 2 - 2 x - 4 y - 6 z - 11 = 0 . Biết rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn (C) là:
A. H 4 ; 4 ; - 1 .
B. H 3 ; 0 ; 2
C. H - 1 ; 4 ; 4
D. H 2 ; 0 ; 3 .
