góc bẹt aOb trên cùng nửa mp bờ ab vẽ hai tia Oc và Od sao cho aOc=bOd=160 độ .Gọi Oe là tia đối của tia Od.Chứng minh rằng bOc=bOe và ob là tia phan giac cua cOe
ai làm đc mình tích
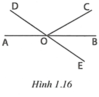
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB. Ta vẽ tia OC và OD sao cho góc AOC = BOD = 160 độ. Gọi tia OE là tia đối của tia OD. Chứng minh rằng:
a) góc BOC = BOE
b) Tia OB là tia phân giác của COE.
a) Ta có:
\(\widehat{DOA}=\widehat{COB}\left(=160^o-\widehat{DOC}\right)\) (1)
Mà \(\widehat{DOA}=\widehat{EOB}\) (2 góc đối đỉnh) (2)
Từ (1) và (2) \(\Rightarrow\widehat{COB}=\widehat{BOE}\left(đpcm\right)\)
b) Vì \(\widehat{COB}=\widehat{BOE}\) (cmt)
\(\Rightarrow OB\) là phân giác của \(\widehat{COE}\)
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ ab ta vẽ 2 tia OC và OD sao cho góc AOC=BOD=160 độ. Gọi OE là tia đối của OD. Chứng minh rằng:
a, BOC=BOE
b, Tia OB là phân giác của COE
Cho góc bẹt AOB . Trên cùng một nửa mp bờ chứa AB ta vẽ 2 tia OC và OD sao cho AOC=BOD=160 . Gọi tia OE là tia đối của tia OD. CM
a) BOC=BOE
B) Tia OB là tia phân giác của góc COE
Ai giải mk tick 2 luôn
a) Ta có tia OE là tia đối của tia OD nên góc BOD và góc BOE là 2 góc kề bù
\(\Rightarrow\)góc DOB+ góc BOE= gócDOE
160độ + góc BOE= 180 độ
góc BOE=180độ-160độ
góc BOE=20độ (1)
Vì góc AOB là góc bẹp nên góc AOB = 180 độ
góc AOC+góc COB=góc AOB
160 độ + góc COB=180 độ
góc COB= 180 đô -160 độ
góc COB= 20 độ (2)
từ (1) và (2) suy ra gócBOC= gócBOE
b) TC: 2 góc EOB và góc BOC là 2 góc kề nhau nên tia OE va tia OC nằm trên 2 nưa mp đối nhau bờ chứa tia OB
suy ra tia OB nằm giữa 2 tia OE và OC
Vì BOC=BOE=20 độ
và tia OB nằm giua 2 tia OE và OC
nên tia OB là tia phân giác của góc COE
Câu viết vào vở thì thay chữ góc và độ bằng kí hiệu nhé
Chúc cậu học tốt k cho mình nhé
Cho góc bẹt AOB . trên cùng nửa mạt phẳng bờ AB . vẽ tia Oc và OD . Sao cho AOC = BOD=140 độ . gọi OE là tia đối của OD
a) Chứng minh BOC = BOE
b) Chứng minh OB là tia phân giác của COE
a)
Vì góc BOD kề bù với góc BOCnên: BOD+BOC=180*
hay: 140*+BOC=180*
=> BOC=180*-140*
Vậy BOC=40*
Vì BOD kề bù với BOEnên: BOD+BOE=180*
hay: 140*+BOE=180*
=> BOE=180*-140*
Vậy BOE=40*
Vậy BOC=BOE=40*
b) Vì BOC=BOE=40*(cmt)
nên: OB là tia phân giác của góc COE
![]() ^...^
^...^ ![]() ^_^
^_^
Cho góc bẹt là aOb,trên cùng một nửa mp bờ ab ta vẽ hai tia Oc và Od sao cho aOc=bOd=30 độ.
a, Hai góc aOc và bOd có phải là hai góc đối đỉnh không.
b, Vẽ tia Oe sao cho tia Ob là tia phân giác của góc dOe. Hai góc aOc và bOe có phải là hai góc đối đỉnh không.
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Oc và OD sao cho góc AOC= góc BOD=135*. Gọi tia OE là tia đối của tia OD. Chứng minh rằng:
a) OC vuông góc với OE.
b) OB là tia phân giác của góc COE.
a) Ta có : \(\widehat{AOC}+\widehat{COB}=180^o\)( kề bù )
\(135^o+\widehat{COB}=180^o\)
\(\widehat{COB}=180^o-135^o\)
\(\widehat{COB}=45^o\)
Ta có : \(\widehat{BOC}+\widehat{COD}=\widehat{BOD}\)
\(45^o+\widehat{COD}=135^o\)
\(\widehat{COD}=135^o-45^o\)
\(\widehat{COD}=90^o\)
Ta có : \(\widehat{DOC}+\widehat{COE}=180^o\)( kề bù )
\(90^o+\widehat{COE}=180^o\)
\(\widehat{COE}=90^o\)
\(\Rightarrow OC\perp OE\)
b) Ta có : \(\widehat{COB}+\widehat{BOE}=\widehat{COE}\)
\(45^o+\widehat{BOE}=90^o\)
\(\widehat{BOE}=90^o-45^o\)
\(\widehat{BOE}=45^o\)
\(\Rightarrow\widehat{BOE}=\widehat{COB}=\frac{\widehat{COE}}{2}\)
Vậy OB là tia phân giác của \(\widehat{COE}\)
Bài giải
Ta có : \(\widehat{AOC}=\widehat{BOD}\left(=135^o\right)\)
\(\widehat{DOC}\) chung và OC và OD cùng nằm trên cùng một nửa mặt phẳng nên \(\widehat{DOA}=\widehat{COB}\)
Mà \(\widehat{DOA}=\widehat{EOB}\) ( hai góc đối đỉnh ) nên \(\widehat{BOC}=\widehat{BOE}\)
\(\Rightarrow\text{ }OB\text{ là tia phân giác }\widehat{COE}\)
Ta có : \(\widehat{BOE}\) và \(\widehat{BOD}\) kề bù nên \(\widehat{BOE}+\widehat{BOD}=180^o\)
\(\Rightarrow\text{ }\widehat{BOE}+135^o=180^o\text{ }\Rightarrow\text{ }\widehat{BOE}=45^o\)
Ta lại có : \(\widehat{COD}+\widehat{COE}=180^o\)
\(\widehat{COD}+90^o=180^o\)
\(\widehat{COD}=90^o\)
\(\text{ }\Rightarrow\text{ }OC\perp OE\)
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia OC và OD sao cho A O C ^ = B O D ^ = 150 ° . Vẽ tia OE là tia đối của tia OD. Chứng tỏ rằng tia OB là tia phân giác của góc COE
Hai góc AOC và BOC kề bù nên A O C ^ + B O C ^ = 180 °
⇒ B O C ^ = 180 ° − 150 ° = 30 ° .
Tương tự, ta tính được A O D ^ = 30 ° .
Ta có B O E ^ = A O D ^ = 30 ° (hai góc đối đỉnh).
Suy ra B O C ^ = B O E ^ = 30 ° . (1)
Tia OB nằm giữa hai tia OC và OE. (2)
Từ (1) và (2) ta được tia OB là tia phân giác của góc COE
Đếm góc, đếm tia
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia OC, OD sao cho AOC =BOD=150 độ .Vẽ tia OE là tia đối của OD. CMR OB là tia phân giác của COE
góc AOC+góc BOC=180 độ
=>góc BOC=180-150=30 độ
góc AOD+góc BOD=180 độ
=>góc AOD=180-150=30 độ
góc AOD=góc BOE(hai góc đối đỉnh)
góc AOD=góc BOC(=30 độ)
=>góc BOC=góc BOE
=>OB là phân giác của góc COE
Để chứng minh OB là tia phân giác của COE, ta cần chứng minh OB cắt góc COE thành hai góc bằng nhau. Gọi M là trung điểm của OD. Ta có: - Góc AOC = 150 độ (theo đề bài) - Góc BOD = 150 độ (theo đề bài) - Góc COE = 180 độ - góc AOC = 180 độ - 150 độ = 30 độ (do AOC là góc bẹt) - Góc DOE = 180 độ - góc BOD = 180 độ - 150 độ = 30 độ (do BOD là góc bẹt) Vì góc COE = góc DOE = 30 độ, nên ta có: - Góc COM = góc DOM = 30 độ (do M là trung điểm của OD) - Góc COB = góc DOB = 150 độ (do OC và OD là hai tia đối của nhau) Vậy ta có: - Góc COM = góc COB = 30 độ - Góc DOM = góc DOB = 30 độ Do đó, OB là tia phân giác của COE.
cho góc bẹt AOB . Trên cùng một nửa mặt phẳng Ab vẽ các tia OC, OD . sao cho góc AOC + BOD =135 độ. Gọi OE là tia đối của OD
a, chứng minh OC vuông góc với OE
b, chứng minh rằng OB là tia phân giác của góc COE