Vẽ 2 đường thẳng a,b vuông góc tại I.Trên đường thẳng a lấy các điểm A,B phân biệt sao cho IA=IB,trên đường thẳng b lấy các điểm C,D sao cho IC=ID. Tìm các đường trung trực trong hình vẽ
Vẽ hình vs nha giúp mik vs
Vẽ hai đường thẳng a và b vuông góc với nhau tại I. Trên đường thẳng a lấy hai điểm A và B sao cho IA= IB; trên đường b lấy các điểm C và D sao cho IC=ID. Tìm các đường trung trực trong hình vẽ
Bạn nào trả lời nhanh mình tick cho![]()
Ta có hình vẽ:
+ Trên đường thẳng a, đoạn IA = IB => I là trung điểm của đoạn AB
Mà đường thẳng a vuông góc với b
=> IC là đường trung trực của đoạn thẳng AB; ID là đường trung trực của đoạn thẳng AB
+ Trên đường thẳng b, đoạn IC = ID => I là trung điểm của đoạn thẳng CD
Mà đường thẳng a vuông góc với b
=> IA là đường trung trực của đoạn thẳng CD; IB là đường trung trực của đoạn thẳng CD
Cho 2 đường thẳng a và b vuông góc với nhau tại M. Trên đường thẳng a lấy 2 điểm A,B phân biệt sao cho MA=MB.Trên đường thẳng b lấy C,D phân biết sao cho MC=MD.Tìm các đường trung trực trong hình vẽ
Bài 1:Cho đường thẳng mn vuông góc với ab tại I. Trên Im lấy điểm A sao cho IA=4 cm.Trên tia Ib lấy điểm C sao cho IC=3 cm.Trên tia Ia lấy điểm D sao cho ID=3 cm.
a) Tính AC và AD;DC.
b) Qua A kẻ đường thẳng xy sao cho xy vuông góc mn.Chứng minh xy // ab
vẽ hộ mk cả hình nha.Nhanh mk tick cho :))))
4)cho tam giác ABC ( AB <AC ). Trên tia đối của tia CA lấy điểm D sao cho CD=AB. Các đường trung trực của các đoạn thẳng BC và AD cắt nhau tại I. chứng minh rằng:
a) IA=ID;IB=IC
b) tam giác IAB= tam giác IDC
c)AI là tia phân giác cảu góc BAC
5)cho tỉ lệ thức: \(\dfrac{a}{b}=\dfrac{c}{d}\). chứng minh rằng ta có tỉ lệ thức sau : \(\left(\dfrac{a+b}{c+d^{ }}\right)^2\)= \(\dfrac{a^2+b^2}{c^2+d^2}\)
5. ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\) \(a.b=c.d\)
\(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{\left(a+b\right)^2-2ab}{\left(c+d\right)^2-2cd}\)
Mà a+b = c+ d; ab = cd
=> đfcm
Bài 4:
a: Ta có: I nằm trên đường trung trực của AD
nên IA=ID
Ta có: I nằm trên đường trung trực của BC
nên IB=IC
b: Xét ΔIAB và ΔIDC có
IA=ID
\(\widehat{AIB}=\widehat{DIC}\)
IB=IC
Do đó: ΔIAB=ΔIDC
Câu 5:
Đặt $\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk$
Khi đó:
$(\frac{a+b}{c+d})^2=(\frac{bk+b}{dk+d})^2=[\frac{b(k+1)}{d(k+1)}]^2=\frac{b^2}{d^2}(1)$
$\frac{a^2+b^2}{c^2+d^2}=\frac{(bk)^2+b^2}{(dk)^2+d^2}=\frac{b^2(k^2+1)}{d^2(k^2+1)}=\frac{b^2}{d^2}(2)$
Từ $(1); (2)\Rightarrow (\frac{a+b}{c+d})^2=\frac{a^2+b^2}{c^2+d^2}$ (đpcm)
Trên tia Ox lấy các điểm A, B sao cho OA=3cm, OB=6cm. Vẽ đường thẳng d vuông góc Ox tại A. Chỉ ra rằng d là đường trung trực của đoạn thẳng OB.
mn giải trình bày thôi nha, mik vẽ hình r
Trên tia Ox, ta có: OA<OB(3cm<6cm)
nên điểm A nằm giữa hai điểm O và B
Suy ra: OA+AB=OB
hay AB=6-3=3(cm)
Ta có: điểm A nằm giữa hai điểm O và B(cmt)
mà OA=AB(=3cm)
nên A là trung điểm của OB
mà d⊥OB tại A
nên d là đường trung trực của OB
Vẽ hai đường thẳng aa' và bb' vuông góc với nhau tại M, trên đường thẳng aa' lấy hai điểm A, B sao cho M là trung điểm của AB. Trên đường thẳng bb' lấy hai điểm C, D sao cho CM=MD. Ghi đầy đủ kí hiệu lên hình vẽ và chứng tỏ đường thẳng bb' là đường trung trực của đoạn thẳng AB và đường thẳng aa' là đường trung trực của đoạn thẳng CD.
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.
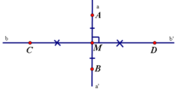
Bài 1. Vẽ đường thẳng m. Lấy A, B, C thuộc m và D không thuộc m. Kẻ các đường thẳng đi qua các cặp điểm.
a) Có bao nhiêu đường thẳng phân biệt? Viết tên các đường thẳng đó.
b) Những đường thẳng nào đồng quy (cùng cắt nhau) tại D?
Bài 2. Đoạn thẳng AB có độ dài 12cm; điểm C nằm giữa hai điểm A và B. Biết rằng CA - CB = 2cm. Tính độ dài các đoạn thẳng CA và CB.
Bài 3. Trên tia Ax lấy hai điểm B và C sao cho AB = 4,5cm, AC = 9cm.
a) Tính độ dài đoạn thẳng BC.
b) Chứng tỏ B là trung điểm của đoạn thẳng AC.
c) Trên tia đối của tia Ax lấy điểm I sao cho A là trung điểm của IB. Tính IC
Bài 1.
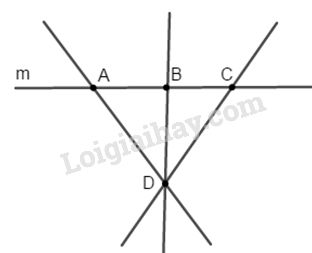
a) Có 4 đường thẳng phân biệt đó là: m, AD, BD và CD.
b) Các đường thẳng cắt nhau tại D là DA, DB và DC.
Bài 2.
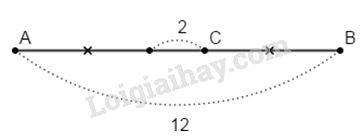
Xem hình vẽ : Ta có:
2CB=12–22CB=12–2
2CB=102CB=10
⇒CB=5(cm)⇒CB=5(cm)
Bài 3.
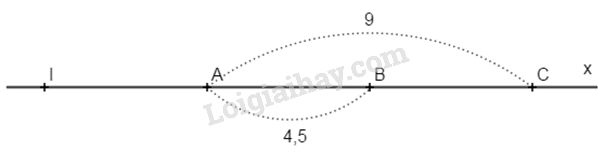
a) Hai điểm B, C thuộc tia Ax mà AB<AC(4,5<9)AB<AC(4,5<9) nên B nằm giữa hai điểm A và C, ta có:
AB+BC=ACAB+BC=AC
4,5+BC=94,5+BC=9
BC=9−4,5=4,5(cm)BC=9−4,5=4,5(cm)
b) B nằm giữa hai điểm A và C và AB=BC=4,5(cm)AB=BC=4,5(cm). Do đó B là trung điểm của đoạn thẳng AC.
c) A là trung điểm của IB nên IA=AB=4,5(cm)IA=AB=4,5(cm).
và AI và AB là hai tia đối nhau. Mặt khác AB, AC, Ax là các tia trùng nhau nên AI và AC là hai tia đối nhau. Do đó A nằm giữa hai điểm I và C.
Ta có: IA+AC=ICIA+AC=IC hay IC=AB+AC=4,5+9=13,5(cm).
Cho điểm M nằm ngoài đường thẳng a, trên đường thẳng a lấy các điểm A, B, C sao cho góc AMB bằng 68 độ, góc BMC=56 độ.
a)vẽ tia MD sao cho MD là tia phân giác của góc AMB(D thuộc đường thẳng a). tính góc DMC
b)trên đường thẳng a lấy thêm một số điểm phân biệt k trùng với các điểm A, B, C. Biết rằng có tất cả 28 đoạn thẳng đi qua 2 điểm là 2 trong số các điểm trên đường thẳng a. tính số điểm đã lấy thêm.
Trình bày rõ ràng nhé ,có hình thì càng tốt
b) Giả sử trên đường thẳng a lấy n điểm thẳng hàng
=> Số đường thẳng tạo thành là \(\frac{n\left(n-1\right)}{2}=28\)
<=> n(n-1)=56=7 x 8
<=> n=8
Vậy số điểm đã lấy thêm là 8-3=5 điểm
Cho tam giác ABC (AB<AC) . Trên tia đối của tia CA lấy điểm D sao cho CD=AB .Các đường trung trực của các đoạn thẳng BC và AD cắt nhau tại I. CM rằng
a) IA=ID, IB=IC
b) tam giác IAB= tam giác IDC
c) AI là tia phân giác của góc BAC
a, I thuộc đường trung trực của AD (Gt)
=> IA = ID (Đl)
I thuộc đường trung trực của BC (gt)
=> IB = IC (đl)
b, xét ta giác IAB và tam giác IDC có : CD = AB (gt)
IB = IC (câu a)
IA = ID (câu a)
=> tam giác IAB = tam giác IDC (c-c-c)
a) I \(\in\) đường trung trực của BC
\(\Rightarrow IB=IC\)
I \(\in\) đường trung trực của AD
\(\Rightarrow IA=ID\Rightarrow\Delta IAD\) cân \(\Rightarrow\widehat{IAC}=\widehat{IDC}\) ( 1 )
Xét \(\Delta IAB\) và \(\Delta IDC\) có :
\(AB=CD\)
\(IB=IC\)
\(IA=ID\)
\(\Rightarrow\Delta IAB=\Delta IDC\)
\(\Rightarrow\widehat{BAI}=\widehat{CDI}\) ( 2 )
Từ (1) và (2) \(\Rightarrow\widehat{BAI}=\widehat{IAC}\Rightarrow AI\) là phân giác của \(\widehat{BAC}\)