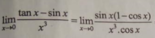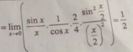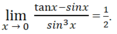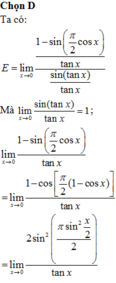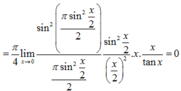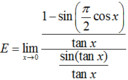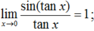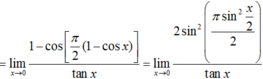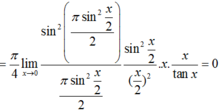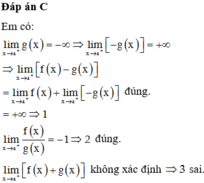Limx->0 tanx/x

Những câu hỏi liên quan
l i m x → 0 tan x - sin x x 3 bằng:
A. 0
B. 2
C. 1/2
D. 1/4
Tính các giới hạn lim x → 0 tan x - sin x sin 3 x
Tìm giới hạn
E
lim
x
→
0
1
-
sin
π
2
cos
x
sin
(...
Đọc tiếp
Tìm giới hạn E = lim x → 0 1 - sin π 2 cos x sin ( tan x ) .
![]()
![]()
![]()
![]()
Tìm giới hạn
E
lim
x
→
0
1
-
sin
π
2
cos
x
sin
(
tan
x...
Đọc tiếp
Tìm giới hạn E = lim x → 0 1 - sin π 2 cos x sin ( tan x )
A. +∞
B. -∞
C. 1
D. 0
1. cho 180 độ x 250 độ. kết quả đúng làA. sinx0, cosx0B. sinx0, cosx0C. sinx0, cosx0D. sinx0, cosx02. cho dfrac{3pi}{4} x dfrac{3pi}{2} kết quả đúng làA. tanx0, cotx0B. tanx0, cotx0C. tanx0, cotx0D. tanx0, cotx03. cho 2pi x dfrac{5pi}{2} kết quả đúng làA. tanx0, cotx0B. tanx0, cotx0C. tanx0, cotx0D. tanx0, cotx04. cho 630 độ x 720 độ. kết quả đúng làA. sinx0, cosx0B. sinx0, cosx0C. sinx0, cosx0D. sinx0, cosx0
Đọc tiếp
1. cho 180 độ < x < 250 độ. kết quả đúng là
A. sinx>0, cosx>0
B. sinx<0, cosx<0
C. sinx>0, cosx<0
D. sinx<0, cosx>0
2. cho \(\dfrac{3\pi}{4}\) <x< \(\dfrac{3\pi}{2}\) kết quả đúng là
A. tanx>0, cotx>0
B. tanx<0, cotx<0
C. tanx>0, cotx<0
D. tanx<0, cotx>0
3.
cho 2\(\pi\) < x <\(\dfrac{5\pi}{2}\) kết quả đúng là
A. tanx>0, cotx>0
B. tanx<0, cotx<0
C. tanx>0, cotx<0
D. tanx<0, cotx>0
4.
cho 630 độ < x <720 độ. kết quả đúng là
A. sinx>0, cosx>0
B. sinx<0, cosx<0
C. sinx>0, cosx<0
D. sinx<0, cosx>0
Giả sử
lim
x
→
a
+
f
(
x
)
+
∞
và
lim
x
→
a
+
g
(
x
)
-
∞
. Xét các mệnh đề sau:
lim
x...
Đọc tiếp
Giả sử lim x → a + f ( x ) = + ∞ và lim x → a + g ( x ) = - ∞ . Xét các mệnh đề sau:
lim x → a + f ( x ) - g ( x ) = + ∞
lim x → a + f ( x ) g ( x ) = - 1
lim x → a + f ( x ) + g ( x ) = 0 . Số mệnh đề đúng là:
A.0
B.1
C.2
D.3
tính giới hạn của các hàm số sau:a, limx→0dfrac{sqrt{1+x}-sqrt{1-x}}{sqrt[3]{1+x}-sqrt{1-x}}b, limx→0(dfrac{1}{x}-dfrac{1}{x^2})c, limx→+∞ dfrac{x^4-x^3+11}{2x-7}d, limx→5 ( dfrac{7}{left(x-1right)^2}.dfrac{2x+1}{2x-3} )
Đọc tiếp
tính giới hạn của các hàm số sau:
a, limx→0\(\dfrac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt[3]{1+x}-\sqrt{1-x}}\)
b, limx→0(\(\dfrac{1}{x}-\dfrac{1}{x^2}\))
c, limx→+∞ \(\dfrac{x^4-x^3+11}{2x-7}\)
d, limx→5 ( \(\dfrac{7}{\left(x-1\right)^2}.\dfrac{2x+1}{2x-3}\) )
a. Áp dụng công thức L'Hospital:
\(\lim\limits_{x\to 0}\frac{\sqrt{x+1}-\sqrt{1-x}}{\sqrt[3]{x+1}-\sqrt{1-x}}=\lim\limits_{x\to 0}\frac{\frac{1}{2}(x+1)^{\frac{-1}{2}}+\frac{1}{2}(1-x)^{\frac{-1}{2}}}{\frac{1}{3}(x+1)^{\frac{-2}{3}}+\frac{1}{2}(1-x)^{\frac{-1}{2}}}=\frac{1}{\frac{5}{6}}=\frac{6}{5}\)
b.
\(\lim\limits_{x\to 0}(\frac{1}{x}-\frac{1}{x^2})=\lim\limits_{x\to 0}\frac{x-1}{x^2}=-\infty\)
Đúng 1
Bình luận (0)
c. Áp dụng quy tắc L'Hospital:
\(\lim\limits_{x\to +\infty}\frac{x^4-x^3+11}{2x-7}=\lim\limits_{x\to +\infty}\frac{4x^3-3x^2}{2}=+\infty \)
d.
\(\lim\limits_{x\to 5}\frac{7}{(x-1)^2}.\frac{2x+1}{2x-3}=\frac{7}{(5-1)^2}.\frac{2.5+11}{2.5-3}=\frac{11}{16}\)
Đúng 1
Bình luận (0)
Biết
lim
x
→
0
f
(
x
)
-
∞
và
I
lim
x
→
0
(
x
-
2
)
3...
Đọc tiếp
Biết lim x → 0 f ( x ) = - ∞ và I = lim x → 0 ( x - 2 ) 3 f ( x ) Khi đó
A. - ∞
B. + ∞
C. -8
D. 0
Cho hàm số y f(x) có
lim
x
→
+
∞
f
(
x
)
0
và
lim
x
→
0
+
f
(
x
)
+
∞
. Khẳng địn...
Đọc tiếp
Cho hàm số y = f(x) có lim x → + ∞ f ( x ) = 0 và lim x → 0 + f ( x ) = + ∞ . Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho không có tiệm cận đứng
B. Trục hoành và trục tung là hai tiệm cận của đồ thị hàm số đã cho
C. Đồ thị hàm số đã cho có một tiệm cận đứng là đường thẳng y = 0
D. Hàm số đã cho có tập xác định là D = (0; +∞)