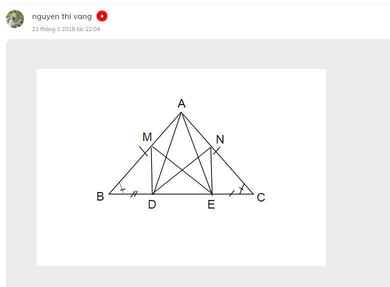
Cho tam giác ABC. Trên cạnh BC lấy điểm D sao cho BD=BA. Trên cạnh AC lấy điểm E sao cho góc ADE= góc ABC. Chứng minh rằng: CE>1/3CA

Những câu hỏi liên quan
Cho tam giác ABC , trên BC lấy D sao cho BA=BD. Trên AC lấy E sao cho góc ABC= góc ADE.
Chứng minh rằng : CE > 1/3AC
1) Cho tam giác ABC vuông tại A ( AB AC ) . Trên tia đối của tia AC lấy điểm D sao cho AD AB. Trên cạnh AB lấy điểm E sao cho AC AEa) Chứng minh rằng : tam giác ABC tam giác ADEb) Gọi M , N lần lượt là trung điểm của DE và BC. Chứng minh tam giác ADM tam giác ABN và tam giác AMN vuông cânc) Qua E kẻ EH vuông góc với BC tại H. Chứng minh rằng 3 điểm D ; E ; H thẳng hàng và CE vuông góc với BD
Đọc tiếp
1) Cho tam giác ABC vuông tại A ( AB > AC ) . Trên tia đối của tia AC lấy điểm D sao cho AD = AB. Trên cạnh AB lấy điểm E sao cho AC = AE
a) Chứng minh rằng : tam giác ABC = tam giác ADE
b) Gọi M , N lần lượt là trung điểm của DE và BC. Chứng minh tam giác ADM = tam giác ABN và tam giác AMN vuông cân
c) Qua E kẻ EH vuông góc với BC tại H. Chứng minh rằng 3 điểm D ; E ; H thẳng hàng và CE vuông góc với BD
Xét ΔADE và ΔABC có :
AD = AB (gt)
góc DAE =góc BAC = 90 độ
AE = AC (gt)
Do đó : ΔADE = ΔABC(c − g − c)
⇒ DE = BC ( hai cạnh tương ứng )
b.
Ta có :
góc ADE =góc CDN ( hai góc đối đỉnh )
góc C= góc E
( vì ΔADE = ΔABC )
⇒ góc N = góc A 90đọ
Hay DE ⊥ BC
Vậy DE ⊥ BC
CẢNH BÁO! Tiếp tục đọc, hoặc linh hồn của bạn sẽ được thực hiện, ngay cả khi bạn đọc từ "cảnh báo"! Có một lần là một người tên là Duke Hunapon. Anh ta lười biếng, và rất bảnh bao. Anh ấy luôn mặc một chiếc áo khoác, không có vấn đề gì ở bên ngoài. Anh ta có một người anh trai tên là Michael, người luôn làm anh ta vây quanh. Một ngày nọ, Michael bị giết, và nó ảnh hưởng rất nhiều đến Duke. Anh ta phát điên và bắt đầu giết người. Chẳng mấy chốc, anh ta đã chiến đấu với ai đó và bị giết. Bây giờ, anh ta đi lang thang xung quanh như một bộ xương cao với một chiếc áo sơ mi màu đỏ, và cùng một chiếc áo hoodie mà Duke đã mặc. Bộ xương này được gọi là "Swapfell Papyrus", và anh ta sẽ giết bạn nếu bạn không đăng bài này trên 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ. Nếu bạn thất bại, và bạn thức dậy khi anh ta ở trong phòng của bạn, cái chết của bạn sẽ chậm và rất đau đớn. Một cô gái tên Lily Lilupanin đọc điều này, và không nghe. Cô bị hãm hiếp và bị giết trong giấc ngủ. Nếu bạn sao chép và dán vào 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ, Swapfell Papyrus sẽ đảm bảo bạn cảm thấy an toàn
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB>AC). Trên tia đối của tia AC lấy điểm D sao cho AD=AB. Trên cạnh AB lấy điểm E sao cho AC=AE.
a) Chứng minh rằng: tam giác ABC = tam giác ADE.
b) Gọi M,N lần lượt là trung điểm của DE và BC. Chứng minh tam giác ADM=tam giác ABN và AMN vuông cân.
c) Qua E kẻ AH vuông góc với BC tại H. Chứng minh rằng 3 điểm D,E,H thẳng hàng và CE vuông góc với BD
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: Xét ΔAMD và ΔANB có
AM=AN
MD=NB
AD=AB
Do đó: ΔAMD=ΔANB
Đúng 0
Bình luận (0)
b1 Cho tam giác ABC có AB = AC. Trên cạnh AB và AC lần lượt lấy hai điểm D và E sao cho AD = AE. Chứng minh rằng góc ADE = góc ABC từ đó suy ra DE // BC.
b2 Cho tam giác ABC đều có ba cạnh bằng 6 cm. Lấy điểm M trên cạnh BC, điểm N trên cạnh AC sao cho MC = NC = 1 cm. Tính chu vi tứ giác ABMN.
B1: \(y=\frac{1}{x^2+\sqrt{x}}\)vì AB=AC=> tam giác ABC cân tại A=> góc B=góc C=> góc B=(180 độ-góc A)/2 (1)
Vì AD=AE=> tam giác ADE cân tại A=> góc ADE=góc AED=> góc ADE=(180 độ-góc A)/2 (2)
Từ (1) và (2)=> góc B=góc ADE
Mà góc B và góc ADE là hai góc đồng vị=> DE//BC
B2: Hình như là 17 cm. Hi hi
Đúng 0
Bình luận (0)
bỏ cái chỗ \(y=\frac{1}{x^2+\sqrt{x}}\) hộ mình cái. mk bấm nhầm
Đúng 0
Bình luận (0)
Bài 8: Cho tam giác ABC, AB AC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD CE. Chứng minh: a) Tam giác ADE cân b) ABD ACEBài 9: Cho tam giác ABC, AB AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD AE. Gọi M là giao điểm của BE và CD. Chứng minh: a) BE CD b) BMD CME. c) AM là tia phân giác của góc BAC. giúp em bài này với ah, em cảm ơn mọi người rất nhiều ( e cần gấp lắm)
Đọc tiếp
Bài 8: Cho tam giác ABC, AB = AC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh: a) Tam giác ADE cân b) ABD = ACE
Bài 9: Cho tam giác ABC, AB = AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh: a) BE = CD b) BMD = CME. c) AM là tia phân giác của góc BAC.
giúp em bài này với ah, em cảm ơn mọi người rất nhiều ( e cần gấp lắm)
Bài 8:
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó:ΔABD=ΔACE
Suy ra: AD=AE
b: ta có: ΔABD=ΔACE
nên \(\widehat{ADB}=\widehat{AEC}\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE=BA, trên tia BA lấy điểm F sao cho BF=BC. Kẻ BD là tia phân giác của góc ABC(D=AC). Chứng minh rằng:
a)DE vuông góc với BC
b) AD nhỏ hơn DC
c) tam giác ADF= tam giác EDC
a: Xét ΔDAB và ΔDEB có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔDAB=ΔDEB
=>góc DEB=90 độ
=>DE vuông góc BC
b: AD=DE
mà DE<DC
nên AD<DC
c: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
Đúng 1
Bình luận (0)
Cho tam giác ABC cân (AB=AC; góc A tù). Trên cạnh BC lấy điểm D, trên tia đối của CB lấy điểm E sao cho BD = CE. Trên tia đối của CA lấy điểm I sao cho CI = CA.
Câu 1: Chứng minh rằng chu vi tam giác ABC nhỏ hơn chu vi tam giác AMN.
Cho tam giác ABC vuông góc tại A , kẻ BD là tia phân giác của góc ABC , ( D thuộc AC ). Trên cạnh BC lấy điểm E sao cho BEBA.a )chứng minh DE AD b.) trên tia đối của tia AB lấy điểm F sao cho AF CE chứng minh BD vuông góc EFc ) chứng minh AE //FC
Đọc tiếp
Cho tam giác ABC vuông góc tại A , kẻ BD là tia phân giác của góc ABC , ( D thuộc AC ). Trên cạnh BC lấy điểm E sao cho BE=BA.
a )chứng minh DE = AD
b.) trên tia đối của tia AB lấy điểm F sao cho AF = CE chứng minh BD vuông góc EFc ) chứng minh AE //FC
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do dó: ΔBAD=ΔBED
=>DA=DE
b: Sửa đề: BD vuông góc với AE
Ta có: BA=BE
DA=DE
Do đó; BD là trung trực của AE
=>BD vuông góc với AE
c: Xét ΔBFC có BA/AF=BE/EC
nên AE//CF
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy hai điểm D,E sao cho BD=CE<BC/2. Đường thẳng kẻ từ D vuông góc với BC cắt AB ở M, đường thẳng kẻ từ E vuông góc với BC cắt AC ở N. Chứng minh rằng:
a) DM=EN
b) EM=DN
c) Chứng minh tam giác ADE cân.