Chứng minh rằng nN,n1 ta có: 1 -
Đọc tiếp
Chứng minh rằng 
n
N,n
1 ta có:
1
- 
Những câu hỏi liên quan
Chứng minh rằng với mọi số nguyên n, ta có:
1.4 + 2.7 + ⋅ ⋅ ⋅ + n 3 n + 1 = n n + 1 2 (1)
* Với n = 1:
Vế trái của (1) = 1.4 = 4; vế phải của (1) = 1 . ( 1 + 1 ) 2 = 4.
Suy ra Vế trái của (1) = Vế phải của (1). Vậy (1) đúng với n = 1.
* Giả sử (1) đúng với n= k. Có nghĩa là ta có: 1.4 + 2.7 + ⋅ ⋅ ⋅ + k 3 k + 1 = k k + 1 2 2
Ta phải chứng minh (1) đúng với n = k + 1. Có nghĩa ta phải chứng minh:
1.4 + 2.7 + ⋅ ⋅ ⋅ + k 3 k + 1 + k + 1 3 k + 4 = k + 1 k + 2 2
Thật vậy 1.4 + 2.7 + ⋅ ⋅ ⋅ + k 3 k + 1 ⏟ = k k + 1 2 + k + 1 3 k + 4 = k k + 1 2 + k + 1 3 k + 4
= ( k + 1 ) . [ k . ( k + 1 ) + 3 k + 4 ] = ( k + 1 ) . ( k 2 + 4 k + 4 ) = k + 1 k + 2 2 (đpcm).
Vậy (1) đúng với n = k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.
Đúng 0
Bình luận (0)
Chứng minh rằng với n ∈ N*, ta có đẳng thức:
1
2
+
2
2
+
3
2
+
.
.
.
.
+
n
2
n
n
+...
Đọc tiếp
Chứng minh rằng với n ∈ N*, ta có đẳng thức: 1 2 + 2 2 + 3 2 + . . . . + n 2 = n n + 1 2 n + 1 6
+ Với n = 1 :
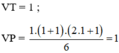
⇒ (3) đúng với n = 1
+ Giả sử đẳng thức (3) đúng với n = k nghĩa là :
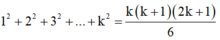
Cần chứng minh (3) đúng khi n = k + 1, tức là:
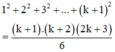
Thật vậy:
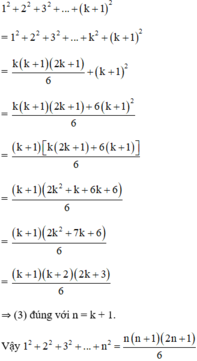
Đúng 0
Bình luận (0)
Cho dãy an=1n([n1]+[n2]+..+[nn])
CHứng minh trong dãy trên có vô hạn n thỏa mãn
a) an+1>an
b) an+1<an
Chứng minh rằng hình n-giác có tất cả n n - 3 2 đường chéo.
Từ mỗi đỉnh của n-giác nối với các đỉnh còn lại ta được n – 1 đoạn thẳng, trong đó có 2 đoạn thẳng là cạnh của hình n-giác (hai đoạn thẳng nối với hai đỉnh kề nhau).
Vậy qua mỗi đỉnh n-giác vẽ được n-3 đường chéo. Hình n-giác có n đỉnh kẻ được n(n- 3) đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy hình n-giác có tất cả n n - 3 2 đường chéo.
Đúng 0
Bình luận (0)
Chứng minh rằng với
n
∈
N
*
thì
1
+
2
+
3
+
.
.
.
+
n
n
n
+
1
2
Đọc tiếp
Chứng minh rằng với n ∈ N * thì 1 + 2 + 3 + . . . + n = n n + 1 2
- Khi n = 1, VT = 1;
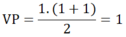
⇒ VT = VP , do đó đẳng thức đúng với n = 1.
- Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là:
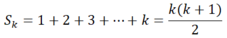
Ta phải chứng minh rằng đẳng thức cũng đúng với n = k + 1, tức là:
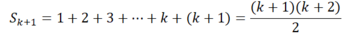
Thật vậy, từ giả thiết quy nạp ta có:
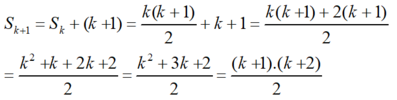
Vậy đẳng thức đúng với mọi n ∈ N*
Đúng 0
Bình luận (0)
Cho đoạn thẳng CDa) Vẽ ba điểm
N
1
,
N
2
,
N
3
sao cho
C
N
1
D
^
C
N
2
D
^...
Đọc tiếp
Cho đoạn thẳng CD
a) Vẽ ba điểm N 1 , N 2 , N 3 sao cho C N 1 D ^ = C N 2 D ^ = C N 3 D ^ = 90 °
b) Chứng minh rằng các điểm N 1 , N 2 , N 3 nằm trên đường tròn đường kính CD.
Vẽ Hình
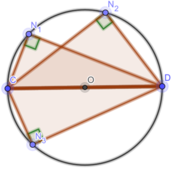
b) Vì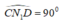 
nên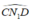 
là góc nội tiếp chắn nửa đường tròn đường kính CD hay
N
1
,
nằm trên đường tròn đường kính CD
Tương tự như vậy ta chứng minh được N 2 , N 3 nằm trên đường tròn đường kính CD
Vậy N 1 , N 2 , N 3 nằm trên đường tròn đường kính CD
Đúng 0
Bình luận (0)
Cho hình vẽ dưới đâya. Chứng minh rằng a // bb. Tính số đo
N
1
^
;
N
2
^
;
N
3
^
;
N
4
^
Đọc tiếp
Cho hình vẽ dưới đây
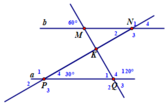a. Chứng minh rằng a // b
b. Tính số đo N 1 ^ ; N 2 ^ ; N 3 ^ ; N 4 ^
a. Q ^ 1 = 60 ° ( kề bù với Q ^ 4 ) mà Q 1 ^ đồng vị với M ^ = 60 ° => a//b
b. Vì a//b N 4 ^ = P ^ 4 = 30 ° ( đồng vị) ⇒ N ^ 1 = N ^ 3 = 150 ° ⇒ N ^ 4 = N ^ 2 = 130 °
Đúng 0
Bình luận (0)
Cho đoạn thẳng CD
Chứng minh rằng các điểm N1, N2, N3 nằm trên đường tròn đường kính CD.
Vì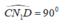 
nên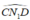 
là góc nội tiếp chắn nửa đường tròn đường kính CD hay N1 nằm trên đường tròn đường kính CD
Tương tự như vậy ta chứng minh được N2,N3 nằm trên đường tròn đường kính CD
Vậy N1,N2,N3 nằm trên đường tròn đường kính CD
Đúng 0
Bình luận (0)
Cho tam giác ABCABC cân tại AA có ˆA=100∘A^=100∘. Lấy điểm MM thuộc cạnh ABAB, điểm NN thuộc cạnh ACAC sao cho AM=AN.AM=AN. Chứng minh rằng MN//BCMN//BC.
Xét ΔABC có
AM/AB=AN/AC
Do đó: MN//BC
Đúng 0
Bình luận (0)