Cho góc xOy < 90 độ, Oz là tia phân giác của góc đó. Trên Oz lấy điểm A, trên Ox và Oy lần lượt lấy 2 điểm B và C sao cho AB = AC. Chứng minh:
a) Góc ABO = góc ACO
b) OB = OA

Những câu hỏi liên quan
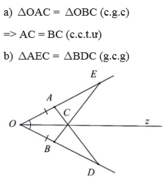
Cho góc \(xOy\) khác góc bẹt, Oz là tia phân giác. Trên các tia Ox, Oy lần lượt lấy các điểm A, B sao cho OA = OB. C là điểm trên tia Oz. Gọi D là giao điểm của AC và Oy, E là giao điểm của BC và Ox. Chứng minh:
a) AC = BC
b) △BCD = △ACE
!!CÓ VẼ HÌNH!!
4. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:
a. Δ AOI = Δ BOI.
b. AB ⊥ OI.
a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
Đúng 1
Bình luận (0)
Cho góc xOy=120 độ. Kẻ tia Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oz lấy điểm B và trên tia Oy lấy điểm C sao cho DA=OB=OC
Chứng minh rằng :
a) OA//CB ; OC//AB
b) OB vuông góc với AC
Cho góc x O y ^ khác góc bẹt, Oz là tia phân, giác. Trên các tia Ox, Oy lần lượt lấy các điểm A, B sao cho OA = OB. C là điểm trên tia Oz. Gọi D là giao điểm của AC và Oy, E là giao điểm của BC và Ox. Chứng minh:
a) AC = BC.
b) ∆ B C D = ∆ A C E
1. Cho góc xOy nhọn và tia phân giác Oz. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA = OB. Lấy điểm I thuộc tia Oz. Chứng minh:
a)△AOI=△BOI
b) AB ⊥ OI
a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
Đúng 2
Bình luận (0)
\(a,\left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OI\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOI=\Delta BOI\left(c.g.c\right)\\ b,\text{Gọi }AB\cap OI=\left\{H\right\}\\ \left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OH\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOH=\Delta BOH\left(c.g.c\right)\\ \Rightarrow\widehat{AHO}=\widehat{BHO}\\ \text{Mà }\widehat{AHO}+\widehat{BHO}=180^0\\ \Rightarrow\widehat{AHO}=\widehat{BHO}=90^0\\ \Rightarrow OI\bot AB\)
Đúng 5
Bình luận (0)
cho góc nhọn xoy oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi I là giao điểm của Oz và AB
a) Chứng minh: Góc BIM = Góc AIN
b) Chứng minh: MN // AB
cho góc nhọn xoy oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi I là giao điểm của Oz và AB
a) Chứng minh: Góc BIM = Góc AIN
b) Chứng minh: MN // AB
M,N ở đâu ra
Đúng 1
Bình luận (0)
cho góc nhọn xoy, oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Gọi I là giao điểm của Oz và AB
a, Chứng minh: tam giác OIA tam giác OIB. Chứng minh Oz và AB
b, Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox, M thuộc Oy). Chứng minh IM IN
c) Chứng minh: Góc BIM Góc AIN
d) Chứng minh: MN // AB
ai làm nhanh cho mình cả bài với ạ
THANK YOU SO MUCH
Đọc tiếp
cho góc nhọn xoy, oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi I là giao điểm của Oz và AB
a, Chứng minh: tam giác OIA = tam giác OIB. Chứng minh Oz và AB
b, Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox, M thuộc Oy). Chứng minh IM = IN
c) Chứng minh: Góc BIM = Góc AIN
d) Chứng minh: MN // AB
ai làm nhanh cho mình cả bài với ạ
THANK YOU SO MUCH
a) Xét tam giác \(OIA\) và tam giác \(OIB\) có:
\(OA=OB\)
\(\widehat{AOI}=\widehat{BOI}\)
\(OI\) cạnh chung
suy ra \(\Delta OIA=\Delta OIB\) (c.g.c)
b) Xét tam giác \(OIN\) và tam giác \(OIM\):
\(\widehat{ION}=\widehat{IOM}\)
\(OI\) cạnh chung
\(\widehat{ONI}=\widehat{OMI}\left(=90^o\right)\)
suy ra \(\Delta OIN=\Delta OIM\) (cạnh huyền - góc nhọn)
\(\Rightarrow IN=IM\)
c) \(\Delta OIA=\Delta OIB\) suy ra \(IA=IB\).
Xét tam giác \(INA\) và tam giác \(IMB\):
\(IA=IB\)
\(\widehat{INA}=\widehat{IMB}\left(=90^o\right)\)
\(IN=IM\)
suy ra \(\Delta INA=\Delta IMB\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow\widehat{AIN}=\widehat{BIM}\)
d) \(\Delta OIN=\Delta OIM\) suy ra \(ON=OM\)
suy ra \(\dfrac{ON}{OA}=\dfrac{OM}{OB}\) suy ra \(MN//AB\).
Đúng 0
Bình luận (0)
Cho góc xOy=120 độ. Kẻ tia Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oz lấy điểm B và trên tia Oy lấy điểm C sao cho DA=OB=OC
Chứng minh rằng :
a) OA//CB ; OC//AB
b) OB vuông góc với AC
Cho góc xOy nhọn và tia phân giác Oz của góc đó. Trên Ox lấy điểm A trên tia Oy lấy điểm B sao cho OA=OB. Gọi C là một điểm trên tia Oz. Chứng minh:
a) AC= BC và góc xAC = góc yBC
b) AB vuông góc với Oz