cho tam giác ABC nhọn có đường cao AH , Kẻ He vuông góc với AB ; kẻ HF vuông góc với AC ; BF cắt HE tại M ; CE cắt HF tại N . Trên BC lấy P và Q sao cho tứ giác FPHN và FQHM nội tiếm . Chứng minh rằng PN = QM

Những câu hỏi liên quan
cho tam giác nhọn ABC, kẻ đường cao AH. từ H kẻ HE vuông góc với AB tại E, kẻ HF vuông góc với AC tại F.
a)chứng minh: tam giác AEH đồng dạng với tam giác AHB
Xét tam giác AEH và tam giác AHB, có:
\(\widehat{AHB}=\widehat{AEH}=90^0\)
\(\widehat{A}:chung\)
Vậy tam giác AEH đồng dạng tam giác AHB ( g.g )
Đúng 3
Bình luận (0)
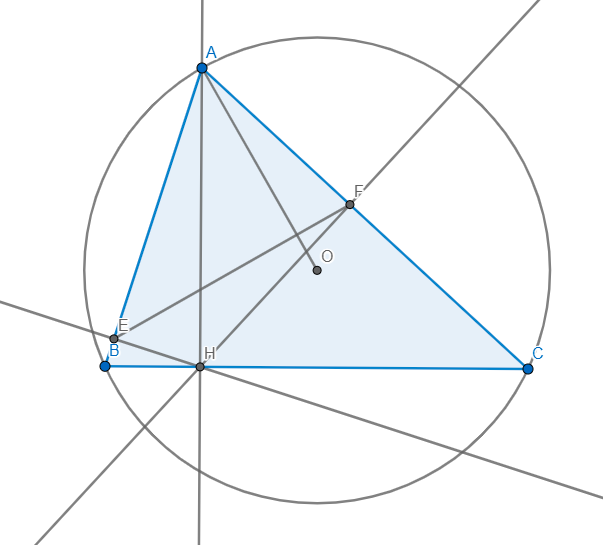
cho tam giác ABC nhọn nội tiếp trong đường tròn tâm O , đường cao AH. Kẻ HE vuông góc với AB , Kẻ HF vuông góc với AC (E thuộc AB,F thuộc AC)
a) CM tứ giác AEHF nội tiếp đường tròn
b) CM góc ABC = góc EFA
c) CM OA vuông góc EF
giúp mình với
a) Ta có: \(\angle AEH+\angle AFH=90+90=180\Rightarrow AEHF\) nội tiếp
b) AEHF nội tiếp \(\Rightarrow\angle EFA=\angle EHA=90-\angle BHE=\angle ABC\)
c) Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle OAC+\angle ABC=90\Rightarrow\angle OAC+\angle AFE=90\Rightarrow OA\bot EF\)
Đúng 1
Bình luận (3)
Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HF vuông góc với AB (F thuộc AB) và kẻ HE vuông góc vói AC (E thuộc AC)a, Chứng minh:
A
F
E
^
A
C
B
^
b, Đường thẳng EF cắt BC tại M. Chứng minh ME.MF MB.MC
Đọc tiếp
Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HF vuông góc với AB (F thuộc AB) và kẻ HE vuông góc vói AC (E thuộc AC)
a, Chứng minh: A F E ^ = A C B ^
b, Đường thẳng EF cắt BC tại M. Chứng minh ME.MF = MB.MC
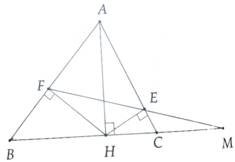
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC
Đúng 0
Bình luận (0)
Cho tam giác ABC(AB<AC) có 3 góc nhọn, kẻ đường cao AH (H thuộc BC). Từ H kẻ HD vuông góc AB và HE vuông góc AC (D thuộc AB, E thuộc AC)
a) C/m: tam giác ADH đồng dạng AHB
b)C/m: AD.AB=AE.AC
a: Xét ΔADH vuông tại D và ΔAHB vuông tại H có
góc DAH chung
=>ΔADH đồg dạng vơi ΔAHB
b: ΔAHB vuông tại H có HD là đường cao
nên AD*AB=AH^2
ΔAHC vuông tại H có HE là đường cao
nên AE*AC=AH^2
=>AE*AC=AD*AB
Đúng 1
Bình luận (0)
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Kẻ đường cao AH, đường kính AD.Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Chứng minh AD vuông góc với EF
Ta có: Tứ giác ABDC nội tiếp đường tròn (O) => ^DBC=^CAD (1)
Đường tròn (O) có đường kính AD và điểm B thuộc (O) => ^ABD vuông tại B => AB \(\perp\)BD
=> HE // BD (Quan hệ song song vuông góc) => ^DBC=^BHE (So le trong)
^BHE=^BAH (Cùng phụ ^AHE) => ^DBC=^BAH=^EAH.
Dễ thấy tứ giác AEHF là tứ giác nội tiếp (Tâm là trung điểm của AH)
=> ^EAH=^EFH. Mà ^EAH=^DBC (cmt) => ^EFH=^DBC (2)
Từ (1) và (2) => ^CAD=^EFH
Lại có: ^EFH+^AFE=900 ; ^CAD+^ADC=900 => ^AFE=^ADC
=> ^CAD+^AFE=900 => AD\(\perp\)EF (đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn có đường cao AH. Kẻ HD vuông góc với AB tại D. Cho AH=8 cm, AB=10 cm
a,Tính HB, HD
b,Kẻ HE vuông góc với AC tại E. CMR: AD.AB=AE.AC
c, Biết góc ACB=30 độ, tính diện tích tứ giác BDEC
Cho tam giác nhọn ABC kẻ đường cao AH từ H kẻ HE vuông góc với AB kẻ HF vuông góc với AC
a, cmr AE.AB=AF.AC
b,AB =5cm AH=7 cm tính AE, BE
c, cho góc HAC =30° tính FC
Cho tam giác nhọn ABC kẻ đường cao AH từ H kẻ HE vuông góc với AB kẻ HF vuông góc với AC
a, cmr AE.AB=AF.AC
b,AB =5cm AH=7 cm tính AE, BE
c, cho góc HAC =30° tính FC
Cho tam giác nhọn ABC kẻ đường cao AH từ H kẻ HE vuông góc với AB kẻ HF vuông góc với AC
a, cmr AE.AB=AF.AC
b,AB =5cm AH=7 cm tính AE, BE
c, cho góc HAC =30° tính FC

















