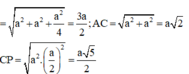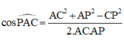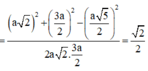cho hình lập phương abcd.a'b'c'd' gọi I là trung điểm cạnh AB. Tính cosin của góc giữa hai đường thẳng A'D và B'I được kết quả là

Những câu hỏi liên quan
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh bằng
2
a
. Gọi K là trung điểm của DD. Tính khoảng cách giữa hai đường thẳng CK và AD. A.
a
3
B.
2
a
5
5...
Đọc tiếp
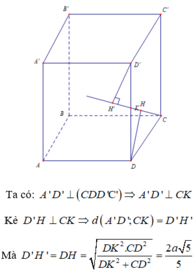
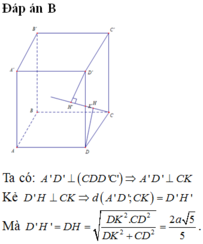
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh bằng 2 a . Gọi K là trung điểm của DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D'.
A. a 3
B. 2 a 5 5
C. 2 a 3 3
D. 4 a 3 3
Cho hình lập phương ABCD.ABCD cạnh bằng 2a. Gọi K là trung điểm của DD. Tính khoảng cách giữa hai đường thẳng CK và AD.
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng 2a. Gọi K là trung điểm của DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D'.
![]()

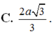
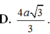
Cho hình lập phương ABCD.ABCD cạnh bằng a. Gọi K là trung điểm DD. Tính khoảng cách giữa hai đường thẳng CK và AD. A. 4a/3 B. a/3 C. 2a/3 D. 3a/4
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi K là trung điểm DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D.
A. 4a/3
B. a/3
C. 2a/3
D. 3a/4
Chọn B
Gọi M là trung điểm BB'. Ta có: CK // A'M => CK // (A'MD)
Khi đó d(CK, A'D) = d (CK, (A'MD)). Gắn hệ trục tọa độ như hình vẽ:
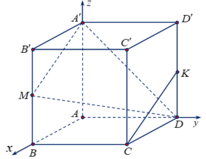
Ta có: A(0;0;0), B(a;0;0), D(0;a;0), A'(0;0;a), B'(a;0;a), C(a;a;0), M(a;0;a/2).
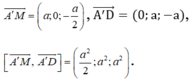
Vậy mặt phẳng (A'MD) nhận ![]() làm vectơ pháp tuyến.
làm vectơ pháp tuyến.
Phương trình (A'MD) là x + 2y + 2z - 2a = 0
Do đó: 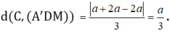
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Gọi K là trung điểm của DD Tính khoảng cách giữa hai đường thẳng CK, AD A.a B.
3
a
8
C.
2
a
5
D.
a
3
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi K là trung điểm của DD' Tính khoảng cách giữa hai đường thẳng CK, A'D
A.a
B. 3 a 8
C. 2 a 5
D. a 3
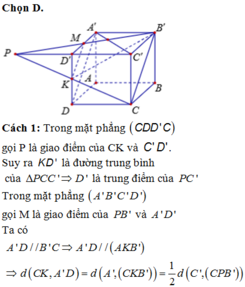
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi K là trung điểm của DD'. Tính khoảng cách giữa hai đường thẳng CK, A'D.
A. a
B. 3 a 8
C. 2 a 5
D. a 3
Chọn D.
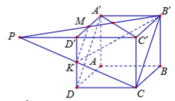
Cách 1: Trong mặt phẳng (CDD'C) gọi P là giao điểm của CK và C'D'.
Suy ra KD' là đường trung bình của ∆ PCC' => D' là trung điểm của PC'.
Trong mặt phẳng (A'B'C'D') gọi M là giao điểm của PB' và A'D'
Ta có ![]()
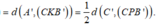
Tứ diện PCC'B' có C'P, C'B và C'B đôi một vuông góc với nhau.
Đặt ![]() thì
thì ![]()
Suy ra ![]()
Vậy ![]()
Cách 2: (Đã học chương 3, HH12)
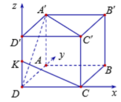
Chọn hệ trục tọa độ sao cho: D(0;0;0), trục Ox trùng với cạnh DC, trục Oy trùng với cạnh DA, trục Oz trùng với cạnh DD', chọn a = 1.
Ta có : ![]()
![]()
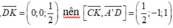
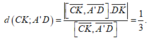
Đúng 0
Bình luận (0)
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a. Gọi K là trung điểm của DD. Khoảng cách giữa hai đường thẳng CK và AD bằng A.
a
3
B.
a
2
C.
a
6
D.
a
3
Đọc tiếp
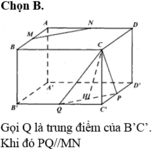
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Gọi K là trung điểm của DD'. Khoảng cách giữa hai đường thẳng CK và A'D bằng
A. a 3
B. a 2
C. a 6
D. a 3
Chọn D.

Phương pháp: Phương pháp tọa độ.
Cách giải: Chọn hệ trục tọa độ như hình vẽ, chọn a = 1


Đúng 0
Bình luận (0)
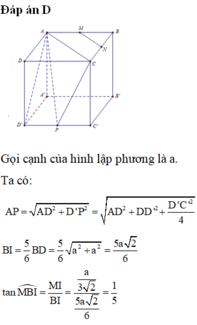
Cho hình lập phương ABCD.A’B’C’D’. Gọi M,N,P lần lượt là trung điểm của các cạnh AB, AD, C’D’. Tính cosin góc giữa hai đường thẳng MN và CP
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’. Gọi M,N,P lần lượt là trung điểm của các cạnh AB, AD, C’D’. Tính cosin góc giữa hai đường thẳng MN và CP
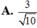
![]()
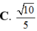
![]()
cho hình lập phương ABCD.A'B'C'D' và M,N,E,F lần lượt là trung điểm các cạnh BC, BA, AA' , A'D'. Tính góc giữa các cặp đường thẳng sau
a) A'C' và BC
b) MN và EF
c) MN và BC
d) EF và CC'
a: ABCD.A'B'C'D' là hình lập phương
=>AA'//BB'//CC'//DD' và AA'=BB'=CC'=DD'
Xét tứ giác AA'C'C có
AA'//CC'
AA'=CC'
Do đó: AA'C'C là hình bình hành
=>AC//A'C'
ABCD.A'B'C'D' là hình lập phương
=>ABCD và A'B'C'D' là hình vuông
ABCD là hình vuông
=>AC là phân giác của góc BAD và CA là phân giác của góc BCD
=>\(\widehat{BAC}=\widehat{DAC}=45^0\) và \(\widehat{BCA}=\widehat{DCA}=45^0\)
\(\widehat{A'C';BC}=\widehat{AC;BC}=\widehat{ACB}=45^0\)
b: Xét ΔBAC có M,N lần lượt là trung điểm của BC,BA
=>MN là đường trung bình của ΔBAC
=>MN//AC
Xét ΔA'AD' có
E,F lần lượt là trung điểm của AA',A'D'
=>EF là đường trung bình của ΔA'AD'
=>EF//AD'
ABCD.A'B'C'D là hình vuông
=>ADD'A' là hình vuông; DCC'D' là hình vuông
ABCD là hình vuông
=>\(AC=AB\cdot\sqrt{2}\)(1)
ADD'A' là hình vuông
=>\(AD'=AD\cdot\sqrt{2}=AB\cdot\sqrt{2}\)(2)
DCC'D' là hình vuông
=>\(CD'=CD\cdot\sqrt{2}=AB\cdot\sqrt{2}\left(3\right)\)
Từ (1),(2),(3) suy ra AC=AD'=D'C
=>ΔAD'C đều
=>\(\widehat{D'AC}=60^0\)
\(\widehat{MN;EF}=\widehat{AC;AD'}=\widehat{CAD'}=60^0\)
c: \(\widehat{MN;BC}=\widehat{AC;CB}=\widehat{ACB}=45^0\)
d: \(\widehat{EF;CC'}=\widehat{AD';DD'}=\widehat{AD'D}=45^0\)
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.ABCD. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CD. Xác định góc giữa hai đường thẳng MN và AP A.
60
0
B.
90
0
C.
30
0
D.
45
0
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, C'D'. Xác định góc giữa hai đường thẳng MN và AP
A. 60 0
B. 90 0
C. 30 0
D. 45 0