Tam giác ABC = Tam giác MNQ, AB=3cm,NQ=4cm,AC=5cm thì MQ có độ dài là

Những câu hỏi liên quan
a) cho tam giác MNQ có MN=2cm , MQ=5cm , NQ=4cm . So sánh các góc của nó. b) Tam giác ERS có góc S=75 độ, góc R=97 độ. Tìm cạnh bé nhất.
a: Xét ΔMNQ có MN<NQ<MQ
nên \(\widehat{Q}< \widehat{M}< \widehat{N}\)
b: \(\widehat{E}=180^0-75^0-97^0=8^0< \widehat{S}< \widehat{R}\)
nên RS là cạnh bé nhất
Đúng 3
Bình luận (1)
a, Vì MN < NQ < NMQ
=> ^Q < ^M < ^N
b, Ta có : ^S + ^R + ^E = 1800 ( tổng 3 góc tam giác )
=> ^E = 1800 - ^S - ^R = 80
Vì ^E < ^S < ^R
=> cạnh bé nhất là SR
Đúng 0
Bình luận (0)
Cho tam giác ABC có độ dài các cạnh
A
B
4
c
m
,
A
C
5
c
m
v
à
B
C
6
c
m
và tam giác MNP có độ dài các cạnh
M
N
3
c
m
,
M
P
2
c
m
,
N
P
...
Đọc tiếp
Cho tam giác ABC có độ dài các cạnh A B = 4 c m , A C = 5 c m v à B C = 6 c m và tam giác MNP có độ dài các cạnh M N = 3 c m , M P = 2 c m , N P = 2 , 5 c m thì:
A. S A B C S M N P = 4
B. S M N P S A B C = 1 2
C. S M N P S A B C = 1 3
Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm. Tam giác MNP đồng dạng với tam giác ABC và diện tích tam giác MNP là 96 c m 2 . Tính độ dài các cạnh của tam giác MNP?
A. 9cm, 12cm, 15cm
B. 12cm, 16cm ; 20cm
C. 6cm, 8cm, 10cm
D. Đáp án khác
![]()
Suy ra: tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
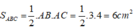
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
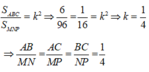
Thay số
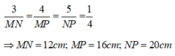
Chọn đáp án B
Đúng 0
Bình luận (0)
cho tam giác ABC với độ dài 3 cạnh AB = 3cm, BC = 5cm, AC = 4cm. Hỏi tam giác ABC là tam giác gì? Tại sao?
cho tam giác ABC có độ dài các cạnh là AB=3cm
Ac=4cm
BC=5cm
chứng minh tam giác đó là tam giác vuông
Theo định lí Pytago đảo thì:
\(3^2+4^2=5^2\)
\(9+16=25\)hợp lí
Vậy tam giác ABC vuông
Đúng 0
Bình luận (0)
Cho tam giác ABC có độ dài các cạnh A B = 5 c m , A C = 3 c m , B C = 4 c m . Tìm góc nhỏ nhất của tam giác
A. Góc A
B. Góc B
C. Góc C
D. Góc B và A
Vì AC là cạnh nhỏ nhất nên góc B là góc nhỏ nhất. Chọn B
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm thì độ dài cạnh BC là:
A. 5cm B. 25cm C.\(\sqrt{5}\)cm D.12cm
Tam giác ABC vuông tại B có độ dài các cạnh lần lượt là: AB = 4cm; BC = 3cm; AC = 5cm. Diện tích tam giác ABC là ...cm2. Số thích hợp điền vào chỗ chấm là
Xem thêm câu trả lời
Tam giác ABC vuông tại A có độ dài các cạnh lần lượt là: AB = 4cm; BC = 3cm; AC = 5cm. Diện tích tam giác ABC là ...cm2. Số thích hợp điền vào chỗ chấm là:
Xem thêm câu trả lời

























