Gọi a,b,\(\sqrt{a^2+b^2}\) lần lượt là độ dài các cạnh của 1 tam giác.
Tìm tỉ số diện tích của đường tròn ngoại tiếp và đường tròn nội tiếp của tam giác đó theo a,b.
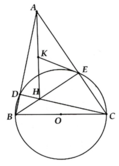
Cho tam giác ABC có B A C ^ = 45 0 , các góc B và C đều nhọn. Đường tròn đường kính BC cắt AB và AC lần lượt tai D và E. Gọi H là giao điểm của CD và BE
a, Chứng minh AE = BE
b, Chứng minh tứ giác ADHE nội tiếp. Xác định tâm K của đường tròn ngoại tiếp tứ giác này
c, Chứng minh OE là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE
d, Cho BC = 2a. Tính diện tích viên phân cung D E ⏜ của đường tròn (O) theo a
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm
Cho tam giác ABC với các cạnh AB = c , AC = b, BC = a . Gọi R , r , S lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và diện tích của tam giác ABC . Trong các phát biểu sau, phát biểu nào sai?
A. S = a b c 4 R
B. R = a sin A
C. D = 1 2 a b sin C
D. a 2 + b 2 - c 2 = 2 a cos C
Cho a, b, c là độ dài ba cạnh của một tam giác với a < b < c và chúng lập thành một cấp số cộng. Chứng minh: a.c = 6.R.r ( R, r lần lượt là các bán kính đường tròn ngoại tiếp và nội tiếp tam giác )
Lời giải:
Vì $a< b< c$ và lập thành 1 csc nên đặt $b=a+d, c=a+2d$.
Theo công thư tính diện tích:
$S=\frac{abc}{4R}=pr$
$\Rightarrow 6Rr=\frac{3abc}{2p}=\frac{3abc}{a+b+c}$
$=\frac{3abc}{a+a+d+a+2d}=\frac{3abc}{3(a+d)}=\frac{3abc}{3b}=ac$ (đpcm)
Cho tam giác ABC và đường tròn tâm I nội tiếp tam giác đó. Gọi A', B', C' lần lượt là các tiếp điểm với cạnh BC, AC, AB. Tính diện tích tam giác A'B'C' theo a, b, c (AB = a, AC = b, BC = c)
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
ho tam giác abc nội tiếp đường tròn (o,r) goi I là tâm của đường tròn nội tiếp tam giác đó gọi M N P lần lượt là tâm của các đường tròn bàng tiếp trong các góc A, B, C. gọi K là điểm đối xứng của I qua O. Chứng minh rằng K laftaam đường tròn ngoại tiếp tam giác MNP
cách làm thôi nha
GỌi D là gia điểm của AM zới đường tròn (O)
CM các tam giác DBI . DBM cân
=> DI=DM
DO đó OD là đường trung bình của tam giác MIK
=> KM=2OD=2R
Zậy M thuộc đường tròn (K;2R)
tương tự đối zới các điểm N , P
Mỗi câu sau đây đúng hay sai?
a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy
d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.
e) Giao điểm ba đường phân giác trong của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
f) Giao điểm ba đường cao của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
g) Tứ giác có tổng độ dài các cặp cạnh đối nhau bằng nhau thì ngoại tiếp được đường tròn
h) Tứ giác có tổng số đo các cặp góc (trong) đối nhau bằng nhau thì nội tiếp được đường tròn.
i) Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó.
Câu a: Đúng Câu b: Sai Câu c: Sai
Câu d: Đúng Câu e: Đúng Câu f: Sai
Câu g: Đúng Câu h: Đúng Câu i: Sai
Cho tam giác ABC và đường tròn tâm I nội tiếp tam giác đó. Gọi A', B', C' lần lượt là các tiếp điểm với cạnh BC, AC, AB. Tính diện tích tam giác A'B'C' theo a, b, c (AB = a, AC = b, BC = c). Không sử dụng vector
Cho tứ diện đều SABC cạnh a. Tỉ số thể tích của hai hình nón cùng đỉnh S, đáy lần lượt là hai đường tròn nội tiếp và ngoại tiếp tam giác ABC là
A. 1 2
B. 1 4
C. 1 3
D. Tỉ số khác
Cho tứ diện đều SABC cạnh a. Tỉ số thể tích của hai hình nón cùng đỉnh S, đáy lần lượt là hai đường tròn nội tiếp và ngoại tiếp tam giác ABC là:
A. 1 2
B. 1 4
C. 1 3
D. Tỉ số khác
Gọi D là tâm đường tròn ngoại tiếp ∆ A B C . Kẻ O H ⊥ A B . Khi đó: V 1 V 2 = O H O A = a 3 6 . 3 a 3 = 1 2
Đáp án A