Cho tam giác ABC cân tại C. Kẻ trung tuyến CM và đường phân giác AD.
Tính số đo góc B biết AD = 2CM
Những câu hỏi liên quan
Cho tam giác ABC cân tại C kẻ trung tuyến CM và đường phân giác AD tính số đo góc B biết AD=2cm
1)Tam giác ABC vuông cân tại A, đường trung tuyến AM. Gọi D là điểm thuộc đoạn thẳng MC. Gọi H là chân đường vuông góc kẻ từ B đến AD. Gọi I, K lần lượt là chân đường vuông góc kẻ từ M đến AD và BH. Chứng minh HM là tia phân giác của góc BHD.2)Tam giác ABC có I là giao điểm các tia phân giác của các góc B và C. Gọi d là giao điểm của AI và BC. Kẻ IH vuông góc với BC( H thuộc BC). Chứng minh rằng góc BIH góc CID.3) Cho tam giác ABC có góc C30 độ. Tia phân giác của góc B và đường phân giác của góc...
Đọc tiếp
1)Tam giác ABC vuông cân tại A, đường trung tuyến AM. Gọi D là điểm thuộc đoạn thẳng MC. Gọi H là chân đường vuông góc kẻ từ B đến AD. Gọi I, K lần lượt là chân đường vuông góc kẻ từ M đến AD và BH. Chứng minh HM là tia phân giác của góc BHD.
2)Tam giác ABC có I là giao điểm các tia phân giác của các góc B và C. Gọi d là giao điểm của AI và BC. Kẻ IH vuông góc với BC( H thuộc BC). Chứng minh rằng góc BIH= góc CID.
3) Cho tam giác ABC có góc C=30 độ. Tia phân giác của góc B và đường phân giác của góc ngoài tại A cắt nhau ở E. Tính số đo góc BCE.
bài toán này cũng dễ mà,nó ra là ... thôi bạn tự là đ
Đúng 0
Bình luận (2)
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
Đúng 0
Bình luận (0)
Bài làm
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau:
5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2.
Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7
Ta làm như sau: 6 - 7
Không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5.
Vậy 8,6 - 2,7 = 5,9
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có AD là đường phân giác a, CM tam giác ADB = tam giác ADC b, kẻ DM vuông góc với AB tại M, DN vuông góc với AC tại N. CM tam giác DMN cân c, Lấy điểm P sao cho D là trung điểm của đoạn thẳng NP. CM đường thẳng BC là đường trung trực của đoạn thẳng MP d, Gọi MP cắt BC tại K, NK cắt MD tại I. CM AD,MN,IP cùng đi qua một điểm
a: Xét ΔADB và ΔADC có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔABD=ΔACD
b: Xét ΔAMD vuông tại M và ΔAND vuông tại N có
AD chung
góc MAD=góc NAD
=>ΔMAD=ΔNAD
=>MD=DN
=>ΔDMN cân tại D
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Qua B kẻ đường thẳng vuông góc với AB. Qua C kẻ đường thẳng vuông góc với AC. Chúng cắt nhau tại D
CM a) tam giác ABC là tam giác cân
b) AD là tia phân giác của góc A và DA là tia phan giác của góc D
c) AD vuông góc với DC và AD đi qua trung điểm của BC
Cho tam giác ABC cân tại A. Kẻ trung tuyến AD. Tia phân giác của góc ADB cắt AB tại E. Tia phân giác của góc ADC cắt AC tại F. Chứng minh:
a) tam giác BED= tam giác CFD
b) AD là trung tuyến của EF
c) BF, CE và AD cắt nhau tại 1đ
Cho tam giác ABC cân tại A. Kẻ trung tuyến AD. Tia phân giác của góc ADB cắt AB tại E. Tia phân giác của góc ADC cắt AC tại F. Chứng minh:
a) tam giác BED= tam giác CFD
b) AD là trung tuyến của EF
c) BF, CE và AD cắt nhau tại 1đ
3 tháng 3 2023 lúc 6:43
cho tam giác ABC cân tại A kẻ từ tia phân giác AD(D thuộc BC) của góc BAC;chưng minh rằng AD là đường trung tuyến của tam giác ABC
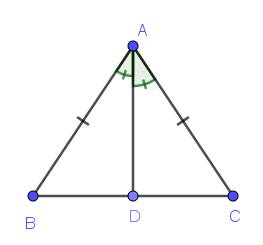
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
AB = AC (gt)
AD là cạnh chung
\(\widehat{BAD}=\widehat{CAD}\) (do AD là tia phân giác)
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow BD=CD\) (hai cạnh tương ứng)
\(\Rightarrow D\) là trung điểm của BC
\(\Rightarrow AD\) là đường trung tuyến của \(\Delta ABC\)
Đúng 3
Bình luận (0)
Ta co: ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường trung tuyến của ΔABC
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại góc A , kẻ AP là phân giác của góc BAC . Hỏi AD có là đường trung tuyến của tam giác ABC không?
Cho tam giác AMN cân tại A. Trên cạnh đáy MN lấy hai điểm B và C sao cho MB NC.a) Chứng minh tam giác ABC cân.b) Vẽ MH vuông góc với đường AB. Vẽ NK vuông góc với đường AC. Chứng minh
∆
M
B
H
∆
N
C
K
.c) Các đường thẳng HM và KN cắt nhau tại O. Tam giác OMN là tam giác gì? Tại sao?d) Khi
B
A
C
^
60
°
và BM CN BC, t...
Đọc tiếp
Cho tam giác AMN cân tại A. Trên cạnh đáy MN lấy hai điểm B và C sao cho MB = NC.
a) Chứng minh tam giác ABC cân.
b) Vẽ MH vuông góc với đường AB. Vẽ NK vuông góc với đường AC. Chứng minh ∆ M B H = ∆ N C K .
c) Các đường thẳng HM và KN cắt nhau tại O. Tam giác OMN là tam giác gì? Tại sao?
d) Khi B A C ^ = 60 ° và BM = CN = BC, tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC
e) Kẻ A D ⊥ B C ( D ∈ B C ) , biết rằng AB =10 cm, BC = 16 cm. Tính độ dài AD.
