Phương trình có số nghiệm là
4
1
3
2

Những câu hỏi liên quan
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau? 1. Phương trình vô nghiệm trên trường số thực R. 2. Phương trình vô nghiệm trên trường số phức C 3. Phương trình không có nghiệm thuộc tập số thực. 4. Phương trình có bốn nghiệm thuộc tập số phức. 5. Phương trình chỉ có hai nghiệm là số phức. 6. Phương trình có hai nghiệm là số thực A. 0. B. 1. C. 3. D. 2.
Đọc tiếp
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Chọn D.
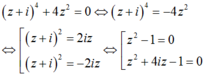
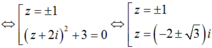
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Đúng 0
Bình luận (0)
Khi giải một hệ phương trình bậc nhất hai ẩn, ta biến đổi hệ phương trình đó để được một hệ phương trình mới tương đương , trong đó có một phương trình một ẩn. Có thể nói gì về số nghiệm của hệ đã cho nếu phương trình một ẩn đó:
a) Vô nghiệm? ; b) Có vô số nghiệm?
a) Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.
b) Hệ đã cho có vô số nghiệm.
Đúng 0
Bình luận (0)
Cho phương trình x2 - (m-1)x-2m-1=0 (1) (m là tham số)
a. Tìm m để phương trình (1) vô nghiệm, có nghiệm, có hai nghiệm phân biệt.
b. Tìm m để phương trình (1) có hai nghiệm phân biệt cùng dương.
c. Tìm m để phương trình (1) có hai nghiệm phân biệt x1 x2 thỏa mãn x12 +x22 =3
a:
\(\text{Δ}=\left(m-1\right)^2-4\left(-2m-1\right)\)
\(=m^2-2m+1+8m+4=m^2+6m+5\)
Để (1) vô nghiệm thì (m+1)(m+5)<0
hay -5<m<-1
Để (1) có nghiệm thì (m+1)(m+5)>=0
=>m>=-1 hoặc m<=-5
Để (1) có hai nghiệm phân biệt thì (m+1)(m+5)>0
=>m>-1 hoặc m<-5
b: Để (1) có hai nghiệm phân biệt cùng dương thì
\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>-1\\m< -5\end{matrix}\right.\\m>1\\m< -\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
Đúng 1
Bình luận (0)
c. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=-2m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=3\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=3\)
\(\Leftrightarrow\left(m-1\right)^2+2\left(2m+1\right)=3\)
\(\Leftrightarrow m^2+2m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=-2\left(loại\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho phương trình m(x-4)-2x=4(1-m) (với m là tham số)
a) Giải phương trình với m=0, m=-1, m=-3
b)Tìm m để phương trình vô nghiệm
c)Tìm m để phương trình có vô số nghiệm
d)Tìm m để phương trình có nghiệm dương duy nhất
e)Tìm m để phương trình có nghiệm duy nhât nhỏ hơn 1
Cho phương trình
y
x
3
-
6
x
2
+
9
x
-
2
và các phát biểu sau:(1) x 0 là nghiệm duy nhất của phương trình(2) Phương trình có nghiệm dương (3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1(4) Phương trình trên có tổng 2 nghiệm là:
-
log...
Đọc tiếp
Cho phương trình y = x 3 - 6 x 2 + 9 x - 2 và các phát biểu sau:
(1) x = 0 là nghiệm duy nhất của phương trình
(2) Phương trình có nghiệm dương
(3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1
(4) Phương trình trên có tổng 2 nghiệm là: - log 5 3 7
Số phát biểu đúng là:
A. 1
B. 2
C. 3
D. 4
Cho phương trình: (m^2-7m+6)x+m^2-1=0 (với m là tham số)
a)tìm m để phương trình có nghiệm duy nhất.
b)tìm m để phương trình có vô số nghiệm.
c)tìm m để phương trình vô nghiệm.
cho hệ phương trình \(\left\{{}\begin{matrix}4x-my-m-6=0\\mx-y-2m=0\end{matrix}\right.\)
tìm m để : a. hệ phương trình vô nghiệm
b. hệ phương trình có nghiệm duy nhất
c. hệ phương trình có vô số nghiệm
Mệnh đề nào sau đây sai?A. Số phức z a + bi là nghiệm của phương trình
x
2
- 2ax + (
a
2
+
b
2
) 0B. Mọi số phức đều là nghiệm của một phương trình bậc hai với hệ số thựcC. Mọi phương trình bậc hai với hệ số thực đều có hai nghiệm trong tập số phức C (hai nghiệm không nhất thiết phân biệt)D. Mọi phương trình bậc hai...
Đọc tiếp
Mệnh đề nào sau đây sai?
A. Số phức z = a + bi là nghiệm của phương trình x 2 - 2ax + ( a 2 + b 2 ) = 0
B. Mọi số phức đều là nghiệm của một phương trình bậc hai với hệ số thực
C. Mọi phương trình bậc hai với hệ số thực đều có hai nghiệm trong tập số phức C (hai nghiệm không nhất thiết phân biệt)
D. Mọi phương trình bậc hai với hệ số thực có ít nhất một nghiệm thực
Mệnh đề nào sau đây sai?A. Số phức z a + bi là nghiệm của phương trình
x
2
- 2ax + (
a
2
+
b
2
) 0B. Mọi số phức đều là nghiệm của một phương trình bậc hai với hệ số thựcC. Mọi phương trình bậc hai với hệ số thực đều có hai nghiệm trong tập số phức C (hai nghiệm không nhất thiết phân biệt)D. Mọi phương trình bậc hai với hệ số thực có ít nhất một nghiệm thực
Đọc tiếp
Mệnh đề nào sau đây sai?
A. Số phức z = a + bi là nghiệm của phương trình x 2 - 2ax + ( a 2 + b 2 ) = 0
B. Mọi số phức đều là nghiệm của một phương trình bậc hai với hệ số thực
C. Mọi phương trình bậc hai với hệ số thực đều có hai nghiệm trong tập số phức C (hai nghiệm không nhất thiết phân biệt)
D. Mọi phương trình bậc hai với hệ số thực có ít nhất một nghiệm thực











