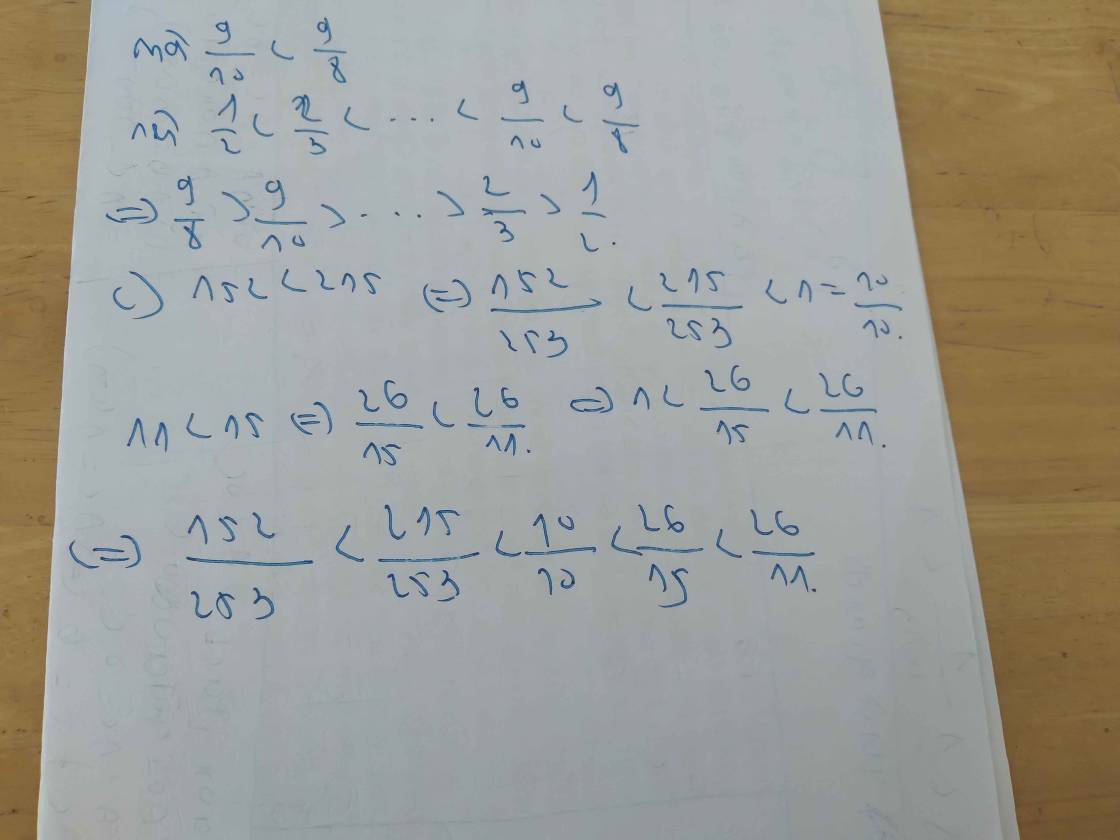1/2 + 1/4 + 1/8 + 1/16 + ............ + 1/152

Những câu hỏi liên quan
viết kết quả bài toán sau:
1/2+1/4+1/8+1/16+1/32+1/64+1/128+1/256+1/152.
Đặt A=1/2+1/4+1/8+1/16+1/32+1/64+1/128+1/256
A=1/21+1/22+1/23+1/24+1/25+1/26+1/27+1/28
1/2A=1/22+1/23+1/24+1/25+1/26+1/27+1/28+1/29
A-1/2A=(1/2+1/22+1/23+1/24+1/25+1/26+1/27+1/28)-(1/22+1/23+1/24+1/25+1/26+1/27+1/28+1/29)
1/2A=1/2-1/29
A=2(1/2-1/29)
A=1-1/28
A=28-1
Đúng 0
Bình luận (0)
a) A=3/4*8/9*15/16+...+899/900 b)B=1/1*2*3+1/2*3*1+1/3*4*5+...+1/98*99*100
c)C=1/2+1/14+1/35+1/65+1/104+1/152 d) D=1/1*2*3*4+1/2*3*4*5+1/3*4*5*6+...+1/27*28*29*30
giải giúp mk
a,
\(A=\left(1-\frac{1}{4}\right)\left(1-\frac{1}{9}\right)...\left(1-\frac{1}{900}\right)\\ =\left(1-\frac{1}{2}\right)\left(1+\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1+\frac{1}{3}\right)...\left(1-\frac{1}{30}\right)\left(1+\frac{1}{30}\right)\\ =\frac{1}{2}\cdot\frac{3}{2}\cdot\frac{2}{3}\cdot\frac{4}{3}\cdot...\cdot\frac{29}{30}\cdot\frac{31}{30}\\ =\frac{1}{2}\cdot\frac{2}{3}\cdot...\cdot\frac{29}{30}\cdot\frac{3}{2}\cdot\frac{4}{3}\cdot...\cdot\frac{31}{30}\\ =\frac{1\cdot2\cdot...\cdot29}{2\cdot3\cdot...\cdot30}\cdot\frac{3\cdot4\cdot...\cdot31}{2\cdot3\cdot...\cdot30}\\ =\frac{1}{30}\cdot\frac{31}{2}=\frac{31}{60}\)
b,
\(B=\frac{1}{2}\left(\frac{2}{1\cdot2\cdot3}+\frac{2}{2\cdot3\cdot4}+...+\frac{2}{98\cdot99\cdot100}\right)\\ =\frac{1}{2}\left(\frac{3-1}{1\cdot2\cdot3}+\frac{4-2}{2\cdot3\cdot4}+...+\frac{100-98}{98\cdot99\cdot100}\right)\\ =\frac{1}{2}\left(\frac{1}{1\cdot2}-\frac{1}{2\cdot3}+\frac{1}{2\cdot3}-\frac{1}{3\cdot4}+...+\frac{1}{98\cdot99}-\frac{1}{99\cdot100}\right)\\ =\frac{1}{2}\left(\frac{1}{2}-\frac{1}{9900}\right)\\ =\frac{1}{2}\cdot\frac{4450-1}{9900}=\frac{1}{2}\cdot\frac{4449}{9900}=\frac{4449}{19800}=\frac{1483}{6600}\)
c, (Chịu :V)
d,
\(D=\frac{1}{3}\left(\frac{3}{1\cdot2\cdot3\cdot4}+\frac{3}{2\cdot3\cdot4\cdot5}+...+\frac{3}{27\cdot28\cdot29\cdot30}\right)\\ =\frac{1}{3}\left(\frac{4-1}{1\cdot2\cdot3\cdot4}+\frac{5-2}{2\cdot3\cdot4\cdot5}+...+\frac{30-27}{27\cdot28\cdot29\cdot30}\right)\\ =\frac{1}{3}\left(\frac{1}{1\cdot2\cdot3}-\frac{1}{2\cdot3\cdot4}+\frac{1}{2\cdot3\cdot4}-\frac{1}{3\cdot4\cdot5}+...+\frac{1}{27\cdot28\cdot29}-\frac{1}{28\cdot29\cdot30}\right)\\ =\frac{1}{3}\left(\frac{1}{6}-\frac{1}{24630}\right)\\ =\frac{228}{4105}\)
Chúc bạn học tốt nha![]() .
.
Đúng 0
Bình luận (0)
B=(1-1/2)+(1-1/4)+(1-1/8)+.......+(1-1/152)+(1-1/1024)+(1-2048)
a) A=3/4*8/9*15/16...899/900 b)B=1/1*2*3+1/2*3*1+1/3*4*5+...+1/98*99*100 c)C=1/2+1/14+1/35+1/65+1/104+1/152 d) D=1/1*2*3*4+1/2*3*4*5+1/3*4*5*6+...+1/27*28*29*30
giair giups mk
A/ viết các phân số sau dưới dạng tỉ số phần trăm 1/2; 1/4;1/8;5/16
B/ Sắp xếp các phân số theo thứ tự giảm dần 1/2; 2/3;3/4; 4/5; 5/6; 6/7; 7/8; 8/9 ; 9/8; 9/10
C/ Sắp xếp các phân số theo thứ tự tăng dần 26/15; 215/253; 10/10; 26/11; 152/253;
Tính nhanh:
a) 153^2+99×153+47^2.
b) 126^2-152×126+5776.
c) 3^8×5^8-(15^4-1)×(15^4+1).
d) (2+1)×(2^2+1)×(2^4+1)...(2^32+1)+1
Ai giúp mình làm bài này với. Mình cảm ơn nhiều.
Đúng 0
Bình luận (0)
a) 153^2+99.153+47^2
= 153^2+2.47.153+47^2
= (153+47)^2
=200^2
=40000
b) 126^2-152.126+5776
= 126^2-2.76.126+76^2
= (126-76)^2
= 50^2
= 2500
c)3^8.5^8-(15^4-1).(15^4+1)
= 15^8-[(15^4)^2-1^2]
= 15^8-15^8+1
=1
d) (2+1).(2^2+1).(2^4+1)...(2^32+1)+1
= 1.(2+1).(2^2+1).(2^4+1)...(2^32+1)+1
= (2-1).(2+1).(2+1).(2^4+1)...(2^32+1)+1
= (2^2-1).(2^2+1).(2^4+1)...(2^32+1)+1
= (2^4-1).(2^4+1)...(2^32+1)+1
= (2^8-1)...(2^32+1)+1
= (2^32-1).(2^32+1)+1
= 2^64-1+1
= 2^64
Đúng 1
Bình luận (0)
rút gọn biểu thức
a) A=16^8 -1/(2+1)(2^2+1)(2^4+1)(2^8+1(3^16+1)
b) B=(3+1)(3^2+1)(3^4+1)(3^8+1)(3^16+1)/9^16-1
giúp mk vs ah mk đang cần gấp ah
a) Ta có: \(A=\dfrac{16^8-1}{\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)}\)
\(=\dfrac{2^{32}-1}{\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)}\)
\(=\dfrac{2^{32}-1}{\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)}\)
\(=\dfrac{2^{32}-1}{\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)}\)
\(=\dfrac{2^{32}-1}{\left(2^{16}-1\right)\left(2^{16}+1\right)}\)
\(=\dfrac{2^{32}-1}{2^{32}-1}=1\)
b) Ta có: \(B=\dfrac{\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{9^{16}-1}\)
\(=\dfrac{\left(3^2-1\right)\cdot\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2\cdot\left(3^{32}-1\right)}\)
\(=\dfrac{\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2\cdot\left(3^{32}-1\right)}\)
\(=\dfrac{\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2\left(3^{32}-1\right)}\)
\(=\dfrac{\left(3^{16}-1\right)\left(3^{16}+1\right)}{2\left(3^{32}-1\right)}=\dfrac{1}{2}\)
Đúng 0
Bình luận (1)
Tính bằng cách thuận tiện nhất: (1+1/2+1/4+1/8+1/16)/(1-1/2+1/4-1/8+1/16)
Bài làm
\(\frac{\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\right)}{\left(1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\frac{1}{16}\right)}\)
\(=\frac{\left(\frac{2}{2}+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}\right)}{\left(\frac{2}{2}-\frac{1}{2}+\frac{1}{2^2}-\frac{1}{2^3}+\frac{1}{2^4}\right)}\)
\(=\frac{\frac{1}{2}\left(2+1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}\right)}{\frac{1}{2}\left(2-1+\frac{1}{2}-\frac{1}{2^2}+\frac{1}{2^3}\right)}\)
\(=\frac{3+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}}{1+\frac{1}{2}-\frac{1}{2^2}+\frac{1}{2^3}}\)
\(=\frac{\frac{24}{8}+\frac{4}{8}+\frac{2}{8}+\frac{1}{8}}{\frac{8}{8}+\frac{4}{8}-\frac{2}{8}+\frac{1}{8}}\)
\(=\frac{31}{8}\div\frac{11}{8}\)
\(=\frac{31}{8}\cdot\frac{8}{11}\)
\(=\frac{31}{11}\)
P/S: Trông không thuận tiện lắm :/
Hawy tính giúp mình nha mình cho đúng
(1+1/2+1/4+1/8+1/16)/(1-1/2+1/4+1/8+1/16)
tính
\(\frac{\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\right)}{\left(1-\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\right)}=\frac{\left(\frac{16}{16}+\frac{8}{16}+\frac{4}{16}+\frac{2}{16}+\frac{1}{16}\right)}{\left(\frac{16}{16}-\frac{8}{16}+\frac{4}{16}+\frac{2}{16}+\frac{1}{16}\right)}=\frac{\frac{31}{16}}{\frac{15}{16}}=\frac{31}{16}:\frac{15}{16}=\frac{31}{16}\times\frac{16}{15}=\frac{31}{15}\)
Đúng 0
Bình luận (0)