Mọi người ơi giúp em vẽ hình và chứng minh bài này với ạ, em cảm ơn rất nhiều ạ.

Mọi người ơi, có thể giúp em bài này và vẽ hình giúp em được không ạ, em cảm ơn rất nhiều ạ.
a:
ΔOBC cân tại O
mà OI là trung tuyến
nên OI vuông góc BC
góc CMO+góc CIO=180 độ
=>CIOM nội tiếp
Mọi người ơi, giúp em bài này với ạ, em cảm ơn rất nhiều ạ.
Gọi vận tốc của ô tô là x
=>Vận tốc xe máy là x-10
Theo đề, ta có: 120/(x-10)-120/x=1
=>(120x-120x+1200)/x(x-10)=1
=>x^2-10x=1200
=>x^2-10x-1200=0
=>x=40
Mọi người ơi, giải giúp em bài này với ạ. Em cảm ơn rất nhiều ạ!
Mọi người ơi, có thể giúp em bài này với không ạ, em cảm ơn rất nhiều ạ.
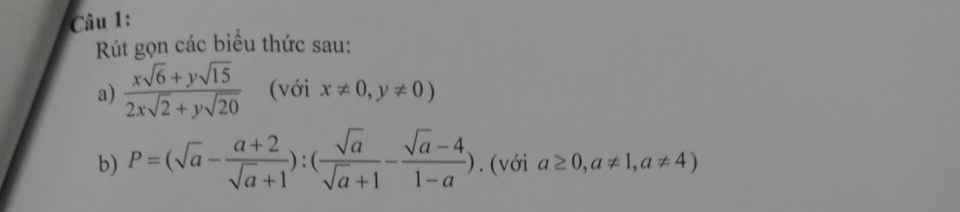
a: \(=\dfrac{\sqrt{3}\left(x\sqrt{2}+y\sqrt{5}\right)}{2\left(x\sqrt{2}+y\sqrt{5}\right)}=\dfrac{\sqrt{3}}{2}\)
b: \(=\dfrac{a+\sqrt{a}-a-2}{\sqrt{a}+1}:\dfrac{a-\sqrt{a}+\sqrt{a}-4}{a-1}\)
\(=\dfrac{\left(\sqrt{a}-2\right)}{\sqrt{a}+1}\cdot\dfrac{a-1}{a-4}=\dfrac{\sqrt{a}-1}{\sqrt{a}+2}\)
Mọi người ơi, giúp em nhanh bài này với ạ, em đang cần gấp lắm ạ. Em cảm ơn rất nhiều ạ!!!!!

Mọi người ơi, giúp em bài này vớ ạ, em đang cần gấp lắm ạ, cảm ơn mng rất rất nhiều ạ.
Mọi người ơi, có thể giúp em giải bài này được không ạ. Em cần gấp lắm ạ.Em cảm ơn rất nhiều ạ.
a: Khi x=2 thì (1) sẽ là:
4-2(m+2)+m+1=0
=>m+5-2m-4=0
=>1-m=0
=>m=1
x1+x2=m+1=3
=>x2=3-2=1
b: Δ=(m+2)^2-4(m+1)
=m^2+4m+4-4m-4=m^2>=0
=>Phương trình luôn có hai nghiệm
P=(x1+x2)^2-4x1x1+3x1x2
=(x1+x2)^2-x1x2
=(m+2)^2-m-1
=m^2+4m+4-m-1
=m^2+3m+3
=(m+3/2)^2+3/4>=3/4
Dấu = xảy ra khi m=-3/2
Mọi người ơi, giúp em rút gọn bài này với ạ!! Em cảm ơn nhiều ạ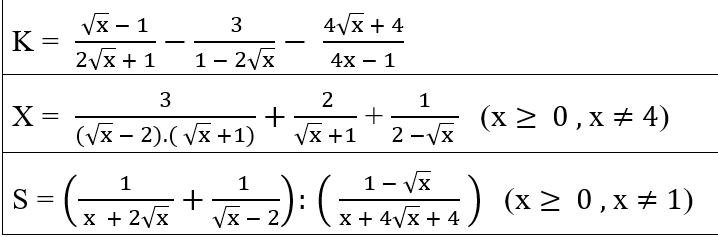
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}+\dfrac{1}{2-\sqrt{x}}\left(đk:x\ge0;x\ne4\right)\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-2}\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{3+2\sqrt{x}-4-\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{1}{\sqrt{x}+1}\)
\(S=\left(\dfrac{1}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}-2}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\left(đk:x\ge0;x\ne1\right)\)
\(S=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\)
\(S=\dfrac{\sqrt{x}-2+x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{x+4\sqrt{x}+4}{1-\sqrt{x}}\)
\(S=\dfrac{x+3\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}\)
\(S=\dfrac{\left(x+3\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\left(1-\sqrt{x}\right)}\)
(đến đoạn này thì trong ngoặc ko tách ra đc nữa nên mik nghĩ là đến đây là xong, nếu sai thì bn nói mik)
\(K=\dfrac{\sqrt{x}-1}{2\sqrt{x}+1}-\dfrac{3}{1-2\sqrt{x}}-\dfrac{4\sqrt{x}+4}{4x-1}\left(đk:x\ge0\right)\)
\(K=\dfrac{\sqrt{x}-1}{2\sqrt{x}+1}+\dfrac{3}{2\sqrt{x}-1}-\dfrac{4\sqrt{x}+4}{4x-1}\)
\(K=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}+\dfrac{3\left(2\sqrt{x}+1\right)}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}-\dfrac{4\sqrt{x}+4}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)
\(K=\dfrac{2x-3\sqrt{x}+1}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}+\dfrac{6\sqrt{x}+3}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}-\dfrac{4\sqrt{x}+4}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)
\(K=\dfrac{2x-3\sqrt{x}+1+6\sqrt{x}+3-4\sqrt{x}-4}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)
\(K=\dfrac{2x-\sqrt{x}}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)
\(K=\dfrac{\sqrt{x}}{2\sqrt{x}+1}\)
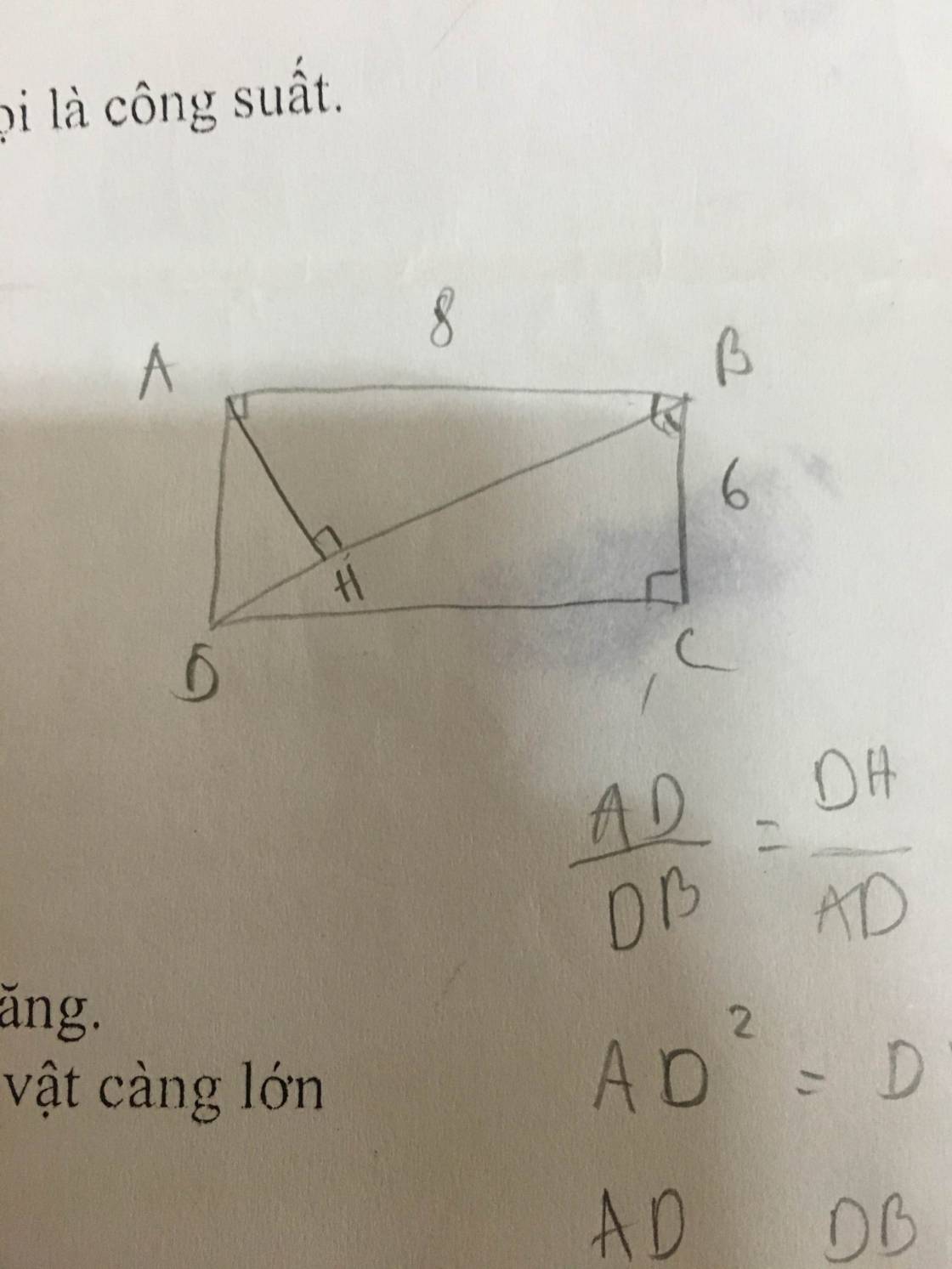
Mọi người giúp em làm bài toán hình này với ạ, kèm vẽ hình luôn nhé ạ. Em cảm ơn nhiều. - Cho hình chữ nhật ABCD có AB=8cm, BC= 6cm. Vẽ đường cao AH của tam giác ABD. a) chứng minh tam giác HBA đồng dạng với tam giác CDB b) Chứng minh: AD^2 = DH. DB c) Tính độ dài đoạn thẳng DH và AH
a.
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)
( sử dụng thước vẽ lại cho chính xác nhé. )
a. xét tam giác HBA và tam giác CDB, ta có :
góc B là góc chung ( gt )
góc H = góc D = 90 độ
do đó : tam giác HBA đồng dạng tam giác CDB ( g - g )
b.
• AD/DB = DH/BC
mà BC = AD ( vì ABCD là hcn )
nên AD/BD = DH/AD
= AD . AD = DB . DH
=> AD^2 = DB . DH ( đpcm )
• vì AB = DC ( ABCD là hcn )
nên DC = 8 cm
áp dụng định lý pytago trong tam giác DBC vuông tại C, ta có:
DB^2 = BC^2 + CD^2
DB^2 = 8^2 + 6^2
DB^2 = 64 + 36
DB^2 = 100
DB = căn bậc 2 của 100
DB = 10 ( cm )
vậy DB = 10 cm