Cho △ ABC cân tại A (A

Những câu hỏi liên quan
Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh rằng :HBHC
b) Chứng minh rằng: AH là tia phân giác của góc A
Bài 2: Cho tam giác ABC cân tại A có góc A 90 độ. Vẽ BM vuông góc với AC tại M, CN vuông góc với AB tại N
a) Chứng minh AM AN
b) Gọi I là giao điểm của BM và CN. Chứng minh rằng AI là tia phân giác của góc A.
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh rằng :HB=HC
b) Chứng minh rằng: AH là tia phân giác của góc A
Bài 2: Cho tam giác ABC cân tại A có góc A < 90 độ. Vẽ BM vuông góc với AC tại M, CN vuông góc với AB tại N
a) Chứng minh AM= AN
b) Gọi I là giao điểm của BM và CN. Chứng minh rằng AI là tia phân giác của góc A.
Cho △ ABC cân tại A (A
Cho tam giác ABC ( góc A < 90 độ) . Vẽ ra phía ngoài tam giác ABC các tam giác vuông cân (cân tại A) Và AEC (cân tại A)
a, CMR : BE=CD
b, Cmr : BE vuông góc với CD
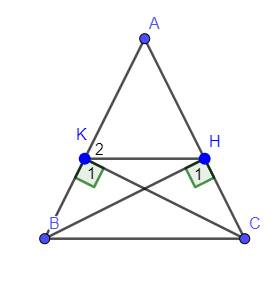
cho tam giác ABC cân tại A ( A < 90˚ ) kẻ BC vuông góc với AC tại H , CK vuông góc với AB tại K
a) chứng minh hai tam giác BHC = CKB từ đó tam giác AHK cân
b) chứng minh BC // HK
`a)`
+, Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=hat(ACB)`
hay `hat(KBC)=hat(HCB)`
Xét `Delta BHC` và `Delta CKB` có :
`{:(hat(H_1)=hat(K_1)(=90^0)),(BC-chung),(hat(HCB)=hat(KBC)(cmt)):}}`
`=>Delta BHC=Delta CKB(c.h-g.n)(đpcm)`
+, Có `Delta BHC=Delta CKB(cmt)`
`=>HC=BK` ( 2 cạnh t/ứng )
mà `AB=AC(Delta ABC` cân tại `A)`
nên `AB-BK=AC-CH`
hay `AK=AH`
`=>Delta AHK` cân tại `A(đpcm)`
`b)`
Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=(180^0-hat(A))/2` (1)
`Delta AHK ` cân tại `A(cmt)=>hat(K_2)=(180^0-hat(A))/2` (2)
Từ (1) và (2) suy ra :
`hat(ABC)=hat(K_2)`
mà `2` góc này ở vị trí Đồng vị
nên `KH////BC(đpcm)`
Đúng 1
Bình luận (0)
Cho tam giác ABC về phía ngoài của tam giác vẽ tam giác BAD vuông cân tại A và tam giác CAE vuông cân tại A.
a) CMR: Đường trung tuyến AM của tam giác ABC vuông góc với DE tại K
b) CMR: Đường cao AH của tam giác ABC đi qua tđ N của DE
Tớ sẽ cho 4 tick, tớ hứa
CHo tam giác ABC cân tại A . Góc ngoài tại đỉnh C có số đo = 125 độ . Tính số đo các góc của tam giác cân đó
http://olm.vn/hoi-dap/question/403871.html
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A. Tia phân giác góc A cẳ BC tại D
a) Chứng minh rắng: Tam giác ADB = tam giác ADC
a: Xét ΔADB và ΔADC có
AD chung
\(\widehat{BAD}=\widehat{CAD}\)
AB=AC
Do đó: ΔADB=ΔADC
Đúng 9
Bình luận (0)
Xét `2 Delta ADB, ADC`:
`AD` chung
`AB = AC`.
`hat(DAB) = hat(DAC)`
`=> Delta ADB = Delta ADC`.
Đúng 5
Bình luận (0)
Xét △ADB và △ADC có:
AD: chung
∠BAD = ∠CAD(AD là tai phân giác)
AB=AC( vì △ABC cân tại A)
⇒ △ADB = △ADC(c.g.c)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A .Vẽ phân giác trong của góc B, và phân giác ngoài của góc A, chúng cắt nhau tại I .Chứng minh rằng AI// BC và tam giác ABI cân
Cho tam giác ABC vuông cân tại A có AB= \(\sqrt{ }\). Về phía ngoài vẽ tam giác ABC vuông cân tại D.
A) Tứ giác ABCD là hình gì? Vì sao ?
B) Tính diện tích ABCD





















