TAM GIÁC ABC VUÔNG TẠI A CÓ AH VUÔNG GÓC BC
CMR AH.BC=AB.AC
cho tam giác abc vuông tại a, đường cao ah. a) Chứng minh: ah.bc = ab.ac, b) be là tia phân giác góc abc, be cắt ah tại d. chứng minh. tam giác abd đồng dạng tam giác cbe
a: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(1\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
b: Xét ΔABD và ΔCBE có
\(\widehat{ABD}=\widehat{CBE}\)(BE là phân giác của góc ABC)
\(\widehat{BAD}=\widehat{BCE}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔABD~ΔCBE
a: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(1\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>\(BC=\sqrt{625}=25\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot25=15\cdot20=300\)
=>\(AH=\dfrac{300}{25}=12\left(cm\right)\)
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(3\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(4\right)\)
Từ (3) và (4) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN đồng dạng với ΔACB
c: Ta có: ΔABC vuông tại A
mà AK là đường trung tuyến
nên AK=KC=KB
Ta có: KA=KC
=>ΔKAC cân tại K
=>\(\widehat{KAC}=\widehat{KCA}\)
Ta có: ΔAMN đồng dạng với ΔACB
=>\(\widehat{ANM}=\widehat{ABC}\)
Ta có: \(\widehat{KAC}+\widehat{ANM}\)
\(=\widehat{ABC}+\widehat{KCA}=90^0\)
=>AK\(\perp\)MN tại I
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2;CH\cdot BC=CA^2\)
=>\(BH\cdot25=15^2=225;CH\cdot25=20^2=400\)
=>BH=225/25=9(cm); CH=400/25=16(cm)
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\)
=>\(AM\cdot15=12^2\)=144
=>AM=144/15=9,6(cm)
Ta có: AMHN là hình chữ nhật
=>AH=MN
mà AH=12cm
nênMN=12cm
Ta có: ΔANM vuông tại A
=>\(AN^2+AM^2=NM^2\)
=>\(AN^2+9,6^2=12^2\)
=>AN=7,2(cm)
Xét ΔIMA vuông tại I và ΔAMN vuông tại A có
\(\widehat{IMA}\) chung
Do đó: ΔIMA đồng dạng với ΔAMN
=>\(\dfrac{S_{IMA}}{S_{AMN}}=\left(\dfrac{AM}{MN}\right)^2=\left(\dfrac{4}{5}\right)^2=\dfrac{16}{25}\)
=>\(S_{IMA}=\dfrac{16}{25}\cdot\dfrac{1}{2}\cdot AM\cdot AN=22,1184\left(cm^2\right)\)
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh:
AH.BC = AB.AC
S = A B C 1 2 A H . B C = 1 2 A B . A C
Þ AH.BC = AB.AC (ĐPCM)
- Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. Gọi AH là đường cao của tam giác ABC. Tính AH? (không sử dụng công thức: AH.BC=AB.AC)
a:
ΔAHC vuông tại H
=>\(AC^2=AH^2+HC^2\)
=>\(AC^2=144\)
=>AC=12(cm)
b: \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)
=>\(AH\cdot BC=AB\cdot AC\)
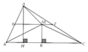
Cho tam giác ABC vuông tại A. Đường cao AH. Cho biết AB=15cm,AC=20cm.
a) Chứng minh AH.BC=AB.AC
b) Tính BC,AH
) Từ H kẻ HE vuông góc với AB ở E và HF vuông góc với AC ở F. Chứng minh tam giác AEF đồng dạng với tam giác ACB
Giải: a) Ta có : \(S_{\Delta ABC}\)= \(\frac{AH.BC}{2}\) (1)
\(S_{\Delta ABC}\)= \(\frac{AB.AC}{2}\) (2)
Từ (1) và (2) suy ra \(\frac{AH.BC}{2}=\frac{AB.AC}{2}\) => AH.BC = AB.AC (Đpcm)
b) Xét t/giác ABC vuông tại A (áp dụng định lí Pi - ta - go)
Ta có: BC2 = AB2 + AC2 = 152 + 202 = 225 + 400 = 625
=> BC = 25
Ta có: AH.BC = AB.AC (cmt)
hay AH. 25 = 15.20
=> AH.25 = 300
=> AH = 300 : 25
=> AH = 12
c) chưa hc
cho tam giác abc vuông tại a . kẻ ah vuông góc với bc . ab=9cm ; ah=7,2cm ; hc = 9,6cm
a) tính ac
b) chứng minh ah.bc=ab.ac
giúp mik ik mik cần gấp lắm
a, Xét △HAC vuông tại H có: CH2 + AH2 = AC2 (định lý Pytago)
=> (9,6)2 + (7,2)2 = AC2 => 92,16 + 51,84 = AC2 => AC2 = 144 => AC = 12 (cm)
b, Ta có: \(S_{\text{△}ABC}=\frac{AC.AB}{2}\)
Và \(S_{\text{△}ABC}=\frac{AH.BC}{2}\)
\(\Rightarrow\frac{AC.AB}{2}=\frac{AH.BC}{2}\)( = S△ABC)
=> AC . AB = AH . BC (đpcm)
Cho tam giác ABC vuông tại A có đường cao AH. Chứng minh:
a. AH2= BH.CH
b. AH.BC= AB.AC
Áp dụng các hệ thức lượng trong tam giác vuông ,ta được:
\(AH^2=BH.CH\)
\(AH.BC=AB.AC\)
Lớp 8 chưa học lượng giác mà??
a) Xét tam giác AHC vuông tại H và tam giác AHB vuông tại H
Áp dụng định lý Pytago cho cả 2 tam giác:
Tam giác AHC: AH^2= AC^2 - CH^2 (1)
TAM GIÁC AHB: AH^2 =AB^2 - BH^2 (2)
(1) (2) Suy ra 2AH^2 = AB^2 + AC^2 - CH^2 - BH^2
2AH^2 = BC^2 - CH^2 - BH^2
2AH^2 = (BH+CH)^2 - CH^2 - BH^2
2AH^2 = 2BH.CH
AH^2 = BH.CH
b) Xét tam giác AHB và tam giác CAB:
H^ = A^ = 90 độ
B^ chung
2 tam giác AHB và tam giác CAB đồng dạng trường hợp (g-g)
Suy ra AH/CA = HB/AB= AB/BC
Vậy AH.BC = AB.AC
Cho tam giác ABC vuông tại A,( AB< AC) đường cao AH( H€BC ).Trên đoạn thằng HC lấy điểm D sao cho HD =HA.Đường vuông góc BC tại D cắt AC tại E.Gọi M là trung điểm của đoạn thẳng BE.Chứng minh:
a) tam giác DEC đồng dạng với tam giác ABC
b) AB.AC=AH.BC