Cho hai số abcdegh và adcbgeh. Hãy chọn một điều kiện để chỉ với điều kiện đó đủ để có: abcdegh adcbgeh.
Đọc tiếp
Cho hai số abcdegh và adcbgeh. Hãy chọn một điều kiện để chỉ với điều kiện đó đủ để có: abcdegh > adcbgeh.
Những câu hỏi liên quan
Câu 4:Trong các mệnh đề sau, mệnh đề nào sai? A. Để tứ giác là hình bình hành, điều kiện cần và đủ là hai cạnh đối song song và bằng nhau. B. Để điều kiện đủ là . C. Để tổng của hai số nguyên chia hết cho 13, điều kiện cần và đủ là mỗi số đó chia hết cho 13. D. Để có ít nhất một trong hai số là số dương điều kiện đủ là .
SGK Cánh diều - Trang 64
29 tháng 3 2023 lúc 23:17
Khi nói về một việc chúng ta có thể nêu điều kiện để việc đó thực hiện. Điều kiện thực hiện một việc cho biết khi nào thì làm, khi nào thì không làm việc đó. Em hãy nói về một việc mà em chỉ làm trong một điều kiện thích hợp.
Ví dụ: Em chỉ mặc áo mưa khi trời mưa, em chỉ xem ti vi sau khi hoàn thành xong bài tập,…
Đúng 0
Bình luận (0)
1.Trong các mệnh đề sau, mệnh đề nào sai ?A. để tứ giác ABCD là hình bình hành, điều kiện cần và đủ là hai cạnh đối song song và bằng nhau.B. Để x^2 25 điều kiện đủ là x 2 .C. Để tổng a + b của hai số nguyên a, b chia hết cho 13, điều kiện đủ là mỗi số đó chia hết cho 13.D. Để có ít nhât một trong hai số a, b là số dương điều kiện đủ là a + b 0 .2.Trong các mệnh đề sau, mệnh đề nào đúng ?A. Để tứ giác T là một hình vuông, điều kiện cần và đủ là nó có bốn cạnh bằng nhau.B. Để tổng hai số tự nh...
Đọc tiếp
1.Trong các mệnh đề sau, mệnh đề nào sai ?
A. để tứ giác ABCD là hình bình hành, điều kiện cần và đủ là hai cạnh đối song song và bằng nhau.
B. Để x^2 = 25 điều kiện đủ là x = 2 .
C. Để tổng a + b của hai số nguyên a, b chia hết cho 13, điều kiện đủ là mỗi số đó chia hết cho 13.
D. Để có ít nhât một trong hai số a, b là số dương điều kiện đủ là a + b > 0 .
2.Trong các mệnh đề sau, mệnh đề nào đúng ?
A. Để tứ giác T là một hình vuông, điều kiện cần và đủ là nó có bốn cạnh bằng nhau.
B. Để tổng hai số tự nhiên chia hết cho 7, là mỗi số đó chia hết cho 7.
C. Để ab > 0, điều kiện cần là cả hai số a và b đều dương.
D. Để một số nguyên dương chia hết cho 3, điều kiện cần là nó chia hết cho 9.
Trong các điều kiện dưới đây, chọn điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B,
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng
Tham khảo:
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng
\( \Leftrightarrow \left\{ \begin{array}{l}AB//AM\\B \; \text {và}\; M \; \text {nằm cùng phía so với điểm A}\end{array} \right.\)
\( \Leftrightarrow \) A, B, thẳng hàng và A nằm giữa B và M
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
TH1: \(MA < MB\)
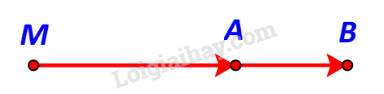
M, A, B thẳng hàng & A nằm giữa M và B.
TH2: \(MA > MB\)
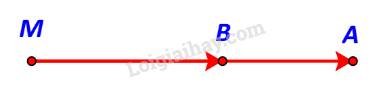
M, A, B thẳng hàng & B nằm giữa M và A.
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
TH1: \(AM < AB\)
A, M, B thẳng hàng & M nằm giữa A và B.
TH2: \(AB < AM\)
A, M, B thẳng hàng & B nằm giữa A và M.
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng
\( \Leftrightarrow \left\{ \begin{array}{l}MA//MB\\A \; \text {và} \; B\; \text {nằm về hai phía so với điểm M}\end{array} \right.\)
\( \Leftrightarrow \) A, M, B thẳng hàng & M nằm giữa A và B.
Vậy điều kiện cần và đủ để M nằm giữa A và B là d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng
Đúng 1
Bình luận (0)
Cho hai đường thẳng phân biệt a, b. Trong các điều kiện sau, điều kiện nào đủ để kết luận được hai đường thẳng a và b song song với nhau A.
a
⫽
P
và
b
⫽
P
B.
a
⫽
c
và
b
⫽
c
C. a và b cùng chéo với đường thẳng c D.
P
⫽
b
và
a
⊂
P
Đọc tiếp
Cho hai đường thẳng phân biệt a, b. Trong các điều kiện sau, điều kiện nào đủ để kết luận được hai đường thẳng a và b song song với nhau
A. a ⫽ P và b ⫽ P
B. a ⫽ c và b ⫽ c
C. a và b cùng chéo với đường thẳng c
D. P ⫽ b và a ⊂ P
Trong các mệnh đề sau mệnh đề nào sai?
A: để tứ giác ABCD là hình bình hành điều kiện cần và đủ là hai cạnh đối song song và bằng nhau
B: để x mũ 2 25 điều kiện đủ là x 5
C: để tổng a + b của hai số nguyên a, bchia hết cho 13 điều kiện cần và đủ là mỗi số đó chia hết cho 13
D: để có ít nhất một trong hai số a,b là số dương điều kiện đủ là a + b0
Mọi người giúp em với ạ
Đọc tiếp
Trong các mệnh đề sau mệnh đề nào sai?
A: để tứ giác ABCD là hình bình hành điều kiện cần và đủ là hai cạnh đối song song và bằng nhau
B: để x mũ 2 = 25 điều kiện đủ là x = 5
C: để tổng a + b của hai số nguyên a, bchia hết cho 13 điều kiện cần và đủ là mỗi số đó chia hết cho 13
D: để có ít nhất một trong hai số a,b là số dương điều kiện đủ là a + b>0
Mọi người giúp em với ạ
Cho số thực m 0. Điều kiện cần và đủ để hai tập hợp
−
∞
;
1
m
và
(
4
m
;
+
∞
)
có giao khác rỗng là: A.
0
m
≤
1
2
B.
0
m
1
2
C.
0
m...
Đọc tiếp
Cho số thực m > 0. Điều kiện cần và đủ để hai tập hợp − ∞ ; 1 m và ( 4 m ; + ∞ ) có giao khác rỗng là:
A. 0 < m ≤ 1 2
B. 0 < m < 1 2
C. 0 < m < 1 4
D. 0 < m ≤ 1 4
Dựa vào hình 52-3A và B kết hợp với hiểu biết của em về quá trình thành lập và ức chế phản xạ có điều kiện, hãy trình bày quá trình thành lập và ức chế phản xạ có điều kiện đã thành lập để thành lập một phản xạ mới qua một ví dụ tự chọn
Vỗ tay mỗi khi thả mồi cho cá ăn, lặp đi lặp lại nhiều lần cho đến khi chỉ nhẹ vỗ tay nhưng không thả mồi cá vẫn nổi lên là ta đã thành lập phản xạ có điều kiện.
Đúng 0
Bình luận (0)
SGK Cánh diều - Trang 25
24 tháng 7 2023 lúc 14:58
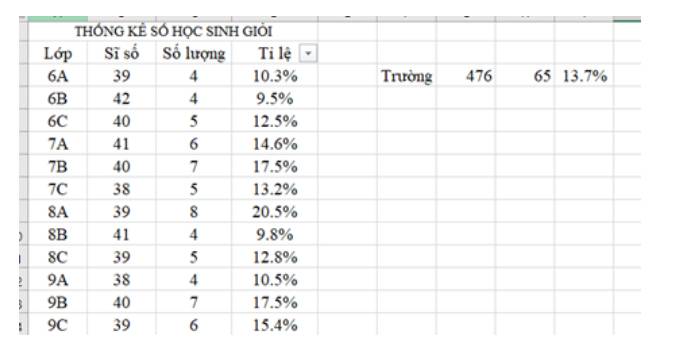
Sử dụng trang tính với bảng dữ liệu trong Hình 1, hãy thực hiện các công việc sau:
- Lọc theo điều kiện để hiển thị chỉ các lớp khối 7 và khối 8.
- Lọc theo điều kiện để hiển thị chỉ các lớp có tỉ lệ số học sinh giỏi của lớp lớn hơn tỉ lệ học sinh giỏi của toàn trường.
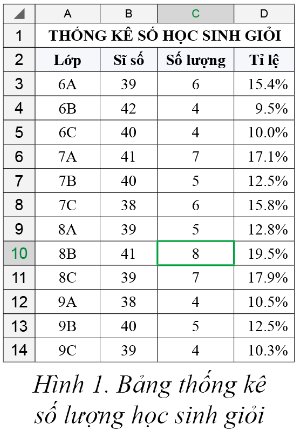
- Để lọc bảng dữ liệu trong Hình 1 để hiển thị chỉ các lớp khối 7 và khối 8, em có thể làm theo các bước sau:
+ Chọn bảng dữ liệu bằng cách nhấp vào một ô bất kỳ trong bảng.
+ Trên thanh menu, chọn "Data" và sau đó chọn "Filter".
+ Trên dòng tiêu đề của cột "Lớp", nhấp vào biểu tượng lọc (hình tam giác) để mở danh sách lọc.
+ Bỏ chọn hết các lớp khác khối 7 và 8 bằng cách nhấp vào ô "Select All" và sau đó bỏ chọn ô của các lớp không phải khối 7 và khối 8.
+ Nhấn nút "OK" để áp dụng bộ lọc.
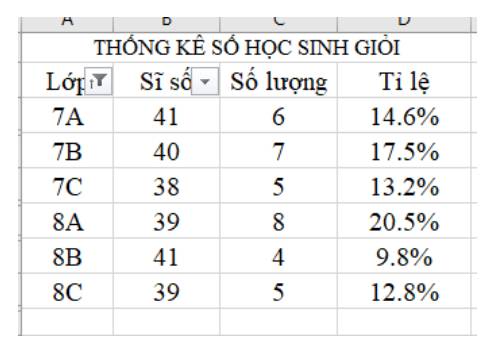
- Lọc theo điều kiện để hiển thị chỉ các lớp có tỉ lệ số học sinh giỏi của lớp lớn hơn tỉ lệ học sinh giỏi của toàn trường.
+ Tính tỉ lệ số học sinh giỏi của toàn trường bằng cách chia tổng số học sinh giỏi cho tổng số học sinh và nhân với 100 để tính phần trăm, sử dụng hàm sum
+ Chọn bảng dữ liệu bằng cách nhấp vào một ô bất kỳ trong bảng.
+ Trên thanh menu, chọn "Data" và sau đó chọn "Filter".
+ Trên dòng tiêu đề của cột "Tỉ lệ (%)", nhấp vào biểu tượng lọc (hình tam giác) để mở danh sách lọc.
+ Chọn "Number Filters" và sau đó chọn "Greater Than" trong danh sách.
+ Trong hộp thoại "Custom AutoFilter", nhập tỉ lệ số học sinh giỏi của toàn trường vào ô "is greater than" và sau đó nhấn nút "OK".
+ Sau khi bộ lọc được áp dụng, chỉ các lớp có tỉ lệ số học sinh giỏi của lớp lớn hơn tỉ lệ học sinh giỏi của toàn trường sẽ được hiển thị trong bảng dữ liệu.
Đúng 0
Bình luận (0)