Cho tam giác ABC vuông tại A. AB = 6cm, AC = 8cm. AD là phân giác của góc A
Tính BD, CD
Cho tam giác ABC vuông tại A, AB=6cm, AC =8cm. Phân giác AD.
a)Tính độ dài BD và CD b) Kẻ DH vuông góc với AB. Tính DH, AD .
Cho tam giác ABC vuông tại A: AB = 6cm, AC = 8cm. Kẻ phân giác trong
BD của góc ABC (D thuộc AC).
a) Tính AD, CD b) Vẽ đường cao AH. Tính AH, HC
c) Tia phân giác góc C cắt BD tại I. Gọi M là trung điểm của BC. Chứng minh
BIM là góc vuông
a)Xét tam giác ABC vuông tại A(gt),có:
AB^2+AC^2=BC^2(Đl pytago)
Thay số:36+64=BC^2
=>BC= căn 100=10cm
Xét tam giác ABC có BD là phân giác góc ABC(gt),có:
AB/AC=AD/DC(Tính chất đường phân giác trong tam giác)
<=>AB/AB+AC=AD/AD+DC(Tính chất tỉ lệ thức)
Thay số:6/16=AD/8
<=>16AD=48
<=>AD=3cm
Vì D thuộc AC(gt)
=>AD+DC=AC
Thay số:3+DC=8
<=>DC=5cm
b) Xét tam giác ABC vuông tại A(gt),có:
SABC=(AB.AC)/2=24cm^2
Mà SABC=(AH.BC)/2
=>(AH.10)/2=24
<=>AH=24.2÷10=4,8cm
Xét tam giác ABC đồng dạng tam giác HAC có:
+Góc C chung
+Góc AHC=góc BAC=90 độ
=>tam giác ABC đồng dạng tam giác HAC(g.g)
=> AH/AB=CH/AC(Cặp cạnh tương ứng)
Thay số : 4,8/6=CH/8
=>CH=4,8.8÷6=6,4cm
c)
Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. Vẽ phân giác BD. Tính AD và CD
cho tam giác ABC vuông tại A biết AB=6cm AC=8cm phân giác của góc A cat cạnh BC tại D tính BD,CD ?
Ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\)
Vì AD là phân giác \(\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\Rightarrow BD=\dfrac{3}{4}CD\)
Ta có: \(BD+CD=BC\Rightarrow\dfrac{3}{4}CD+CD=10\Rightarrow\dfrac{7}{4}CD=10\Rightarrow CD=\dfrac{40}{7}\)
\(\Rightarrow BD=\dfrac{3}{4}.\dfrac{40}{7}=\dfrac{30}{7}\)
Cho tam giác ABC vuông tại A: AB = 6cm, AC = 8cm. Kẻ phân giác trong
BD của góc ABC (D thuộc AC).
a) Tính AD, CD b) Vẽ đường cao AH. Tính AH, HC
c) Tia phân giác góc C cắt BD tại I. Gọi M là trung điểm của BC. Chứng minh
\(\widehat{BIM}\)là góc vuông
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm
b) Phân giác của góc A cắt BC tại D. Tính BD, CD
b) Do AD là tia phân giác của góc BAC, D ∈ BC nên ta có:
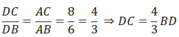
Mặt khác ta lại có:
DC + DB = BC ⇒ (4/3.BD) + BD = 10 ⇒ 7/3.BD = 10 ⇒ BD = 30/7 (cm)
Khi đó:
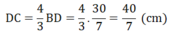
Bài 6:cho tam giác ABC vuông tại A, AB=6cm, AC=8cm. Phân giác AD
a)Tính độ dài BD và CD
b)Kẻ DH vuông góc với AB. Tính DH, AD
a, dùng pytago tính ra BC = 10 cm
tam giác ABC có AD là phân giác (gt)
=> CD/AC = BD/AB (tính chất)
=> CD + DB/AB+AC = CD/AC + BD/AB
AB = 6; AC = 8; BC = 10 và CD + DB = BC
=> 10/14 = CD/8 = BD/6
=> CD = 40/7 và BD = 30/7
Cho tam giác ABC vuông tại A, AB=6cm, AC=8cm đường cao AH tia phân giác góc C cắt AB tại D tính BC , AD , BD
Xét tam giác vuông ABC có:
BC^2=AB^2+AC^2
BC^2=6^2+8^2
BC=√6^2+8^2=10cm
Xét tam giác ABC có CD phân giác:
AD/BD=AC/BC(t/chất đường phân giác )
<=>AD+BD/BD=AC+BC/BC
<=>6/BD=18/10
<=>BD=10.6/18≈3,3cm
Ta có : AD+BD=AB
=>AD=AB-BD=6-3,3=2,7
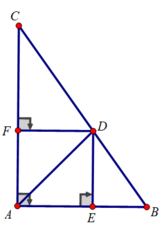
cho tam giác ABC vuông tại A. Phân giác góc BAC cắt cạnh BC tại D kẻ DE vuông góc với AB tại E, kẻ DF vuông góc với AC tại F a, chứng minh AEDF là hình vuông.
b,Gọi M,N lần lượt là trung điểm của BD và CD chứng EMD=2.ABC và EM//FN.
c,cho AB=6cm,AC=8cm. tính diện tích hình vuông AEDF.
a: Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
AD là phân giác của góc FAE
Do đó: AEDF là hình vuông
b: ΔDEB vuông tại E
mà EM là trung tuyến
nên EM=MD
=>góc EMD=2*góc ABC