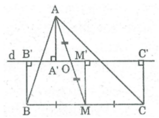
Ta có: BB' ⊥ d (gt)

CC' ⊥ d (gt)

Suy ra: BB'// CC'

Tứ giác BB'C'C là hình thang

Kẻ MM' ⊥ d ⇒ MM' // BB' // CC'

Lại có M là trung điểm của BC nên M' là trung điểm của B’C’

⇒ MM' là đường trung bình của hình thang BB'C'C

⇒ MM' = (BB' + CC') / 2 (1)

* Xét hai tam giác vuông AA'O và MM'O:

∠ (AA'O) =  ∠ (MM' O) = 90 0

AO=MO (gt)

∠ (AOA') =  ∠ (MOM' ) (2 góc đối đỉnh)

Do đó: ∆ AA'O =  ∆ MM'O (cạnh huyền, cạnh góc nhọn)

⇒AA' = MM' (2)

Từ (1) và (2) suy ra: AA' = (BB' + CC') / 2

Ta có: BB’ ⊥ d (gt)

            CC’ ⊥ d (gt)

Suy ra: BB’ // CC’

Tứ giác BB’CC’ là hình thang

Kẻ MM’ ⊥ d

 ⇒ MM’ // BB’ // CC’

Nên MM’ là đường trung bình của hình thang BB’CC’

⇒MM′=BB′+CC′2(1)⇒MM′=BB′+CC′2(1)

Xét hai tam giác vuông AA’O và MM’O:

ˆOA′A=ˆOM′MOA′A^=OM′M^

AO = MO (gt)

ˆAOA′=ˆMOM′AOA′^=MOM′^ (đối đỉnh)

Do đó: ∆ AA’O = ∆ MM’O (cạnh huyền, góc nhọn)

⇒ AA’ = MM’ (2)

Từ (1) và (2) suy ra: AA′=BB′+CC′2AA′=BB′+CC′/2.

Từ M kẻ MH vuông góc với B'C' (H thuộc B'C')

Dễ dàng chứng minh được MH là đường trung bình của hình thang BCC'B'

=> \(MH=\frac{BB'+CC'}{2}\)

Dễ thấy tam giác OAA' = tam giác OHM (cạnh huyền - góc nhọn)

=> AA' = MH

=> \(BB'+CC'=2AA'\)

Bạn xem lại đề bài.

Trên tia đối của MP lấy điểm D sao cho MP=MD.

Ta có: \(\Delta\)MBP=\(\Delta\)MCD (c.g.c) => BP=CD (2 cạnh tương ứng)

Mà BP=CQ => CD=CQ  => \(\Delta\)DCQ cân tại C => ^CQD= (180⁰-^DCQ)/2

=> ^MPB=^MDC (2 góc tương ứng) ở vị trí so le trong => AB//CD => ^DCQ=^IAK (Đồng vị) 

M là trung điểm PD, N là trung điểm PQ => MN là đường trung bình của \(\Delta\)PDQ

=> MN//DQ hay IK//DQ => ^CQD=^AKI (Đồng vị) 

 => \(\Delta\)AIK có: ^AKI= (180⁰-^IAK)/2 = (180⁰-^DCQ)/2 = ^CQD

=> Tam giác AIK cân tại A (đpcm)

I. Nội qui tham gia "Giúp tôi giải toán"

1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;

2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.

3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.

Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

Bạn NX Toàn ơi, bạn bị rảnh ạ, rớt hết phần duyên ra rồi🙃🙃🙃