cho hình vẽ: CMR:CF+BK<AC+AB

Những câu hỏi liên quan
Có ai bk vẽ hình không? chỉ cho mk với
Trên này có nhều đứa biết vẽ lắm
Đúng 0
Bình luận (0)
Nguyễn Minh Anh bảo mấy bn CTV chỉ cho , phần này mk cx ko rành lắm
Đúng 0
Bình luận (0)
Cho a, A và B\(\notin\)a . vẽ AH vuông góc với a và BK Vuông góc với a.Hỏi AH có song song với BK k? vì sao?Vẽ hình nha
Có vì hai góc tạo ra những góc đồng vị và so le
Đúng 0
Bình luận (0)
Cho tam giác ABC. Hãy kẽ
- CF vuông góc với AB
- BE vuông góc với AC
Biết AB<AC
CMR:CF>BE
Cho hình vuông ABCD. Vẽ bên ngoài hình vuông DEGH. HE cắt BC tại K. So sánh BK và DE?
cho tam giac ABC co MC = 1/4 BC ,
BK là đường cao của tam giác ABC
MH đường cao của tam giác AMC có.
AC là dạy chúng . so sánh độ dài BK và MH .
có hình vẽ nhưng hình vẽ khó quá nên ko vẽ được.
Cho hình vẽ sau: A M W B P G K L Q S S nằm trong ▲ABK. MG // AK ; BK // WL ; AB // PQ. MG, PQ và WL đồng quy tại S.Tính 2left(dfrac{BW}{AB}+dfrac{GK}{BK}right)+dfrac{WS}{BK}+dfrac{AQ}{AK}.
Đọc tiếp
Cho hình vẽ sau:
S nằm trong ▲ABK. MG // AK ; BK // WL ; AB // PQ. MG, PQ và WL đồng quy tại S.
Tính \(2\left(\dfrac{BW}{AB}+\dfrac{GK}{BK}\right)+\dfrac{WS}{BK}+\dfrac{AQ}{AK}\).
Tứ giác AMSQ có: AM // SQ ; MS // AQ} gt
⇔ Tứ giác AMSQ là hình bình hành ⇒ AM = SQ
Tứ giác BWSP có: BW // SP ; BP // WS} gt
⇔ Tứ giác BWSP là hình bình hành ⇒ BW = SP
Tứ giác GSLK có: GK // SL ; GS // KL} gt
⇔ Tứ giác GSLK là hình bình hành ⇒ GK = LS
+) \(SQ + SP = PQ(gt) \) trong khi \(AM = SQ ;BW = SP \)
\(⇔ AM + BW = SQ + SP = PQ\)
+) \(2GK + WS = WS + SL + GK\) (vì GK = LS) \(= WL + GK\)
Vì ▲ABK có MG // AK; WL // BK và M,W ∈ AB; G ∈ BK; L ∈ AK nên:
\(+)\frac{WL}{BK} = \frac{AW}{AB} \) (Định lý Talet)
\(+)\frac{BG}{BK} = \frac{MB}{AB}\) (Định lý Talet) \(⇔\frac{BK - GK}{BK} = \frac{AB - AM}{AB}\)
\(⇔ 1 – \frac{GK}{BK} = 1 – \frac{AM}{AB} \)
\(⇔ \frac{GK}{BK} = \frac{AM}{AB}\)
Vì ▲ABK có PQ // AB và P ∈ BK; Q ∈ AK nên: \(+) \frac{QK}{AK} = \frac{PQ}{AB} \) (Định lý Talet)
\(⇔1 – \frac{QK}{AK} = 1 – \frac{PQ}{AB}\)
\(⇔ \frac{AK-QK}{AK} = \frac{AB-PQ}{AB} \)
\(⇔ \frac{AQ}{AK} = \frac{AB-PQ}{AB}\)
\(+) 2(\frac{BW}{AB}+\frac{GK}{BK})+\frac{WS}{BK}+\frac{AQ}{AK} = \frac{2BW}{AB}+\frac{2GK}{BK}+\frac{WS}{BK}+\frac{AQ}{AK} \)
\( = \frac{2BW}{AB}+\frac{WL + GK}{BK}+\frac{AQ}{AK}\)
Với \(\frac{GK}{BK} = \frac{AM}{AB} ; \frac{WL}{BK} = \frac{AW}{AB}; \frac{AQ}{AK} = \frac{AB-PQ}{AB}\) , ta có:
\(\frac{2BW}{AB}+\frac{WL}{BK}+\frac{GK}{BK}+\frac{AQ}{AK} \)
\(= \frac{BW + BW}{AB}+\frac{AW}{AB}+\frac{AM}{AB}+\frac{AB - PQ}{AB}\)
\(= \frac{AB + BW + AW + AM + BW – PQ}{AB}\)
\(= \frac{AB + AB + PQ – PQ}{AB} \)
\(= \frac{2AB}{AB} = 2\)
➤ \(2(\frac{BW}{AB}+\frac{GK}{BK})+\frac{WS}{BK}+\frac{AQ}{AK}\) \(=2\)
Đúng 3
Bình luận (0)
Mình phải hết sức khó khăn với bài tập kiểu này.
Đúng 3
Bình luận (1)
Cho hình chóp SABC có SA \(\perp\) (ABC). Vẽ BH \(\perp\)AC và BK \(\perp\) SC. CM: SC \(\perp\)(BHK)
BH vuông góc AC
BH vuông góc SA
=>BH vuông góc (SAC)
=>BH vuông góc SC
SC vuông góc BK
SC vuông góc BH
=>SC vuông góc (BHK)
Đúng 0
Bình luận (0)
cho hình chữ nhật ABCD kẻ BK vuông góc với AC láy M,N lần lượt là trung điểm của AK,DC kẻ CI vuông góc với BM (I∈BM) và CI cắt BK tại E .cmr a,vẽ hình
b,EB=EK
c,tứ giác MNCE là hình bình hành
d,MN⊥BM
a: 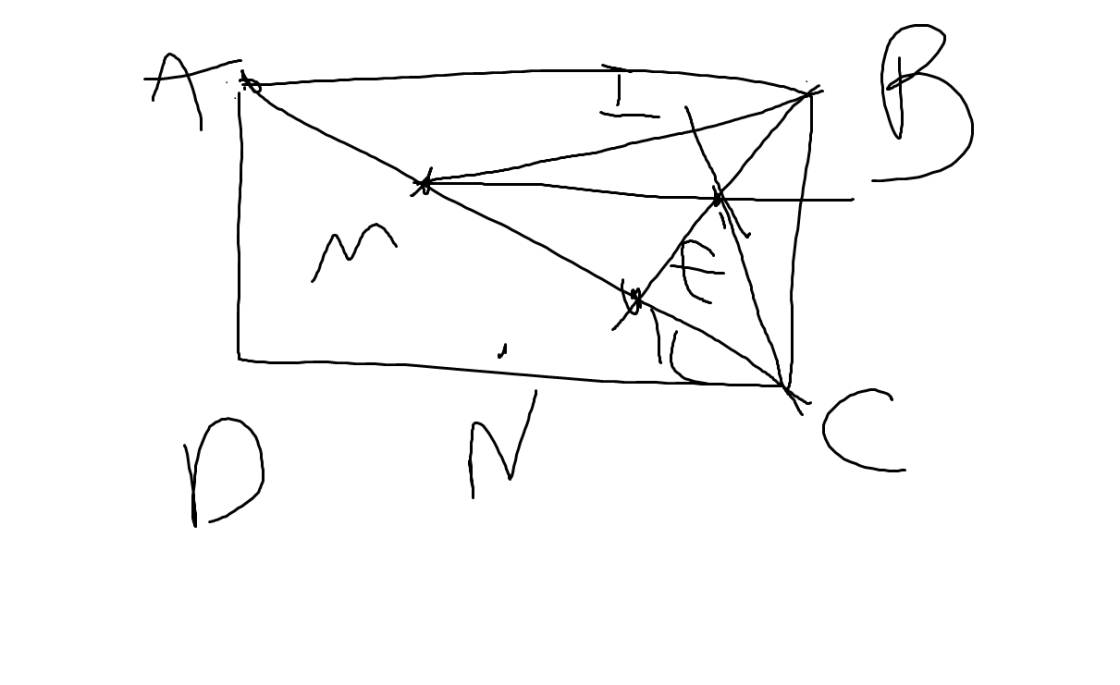
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB
Đúng 0
Bình luận (0)
Giúp với,mình cần gấp ạ!
Cho hình bình hành ABCD,vẽ BH vuông AD,BK vuông DC.Biết rằng BH = BK.Chứng minh rằng ABCD là hình thoi

















