Cho nửa đường tròn tâm O đường kính AB, dây CD các đường vuông góc với C,D tại C, D cắt AB ở E, F
a, Chứng minh rằng E đối xứng với F qua O
b, tính S tứ giác CDFE biết AB=5 cm CD=14cm
Cho nửa đường tròn tâm O đường kính AB, dây CD các đường vuông góc với C,D tại C, D cắt AB ở E, F .Tính S tứ giác CDFE biết AB=50 cm CD=14cm
Kẻ OH vuông góc CD
=>H là trung điểm của CD
Xét hình thang EFDC có
H là trung điểm của CD
HO//CE//DF
=>O là trung điểm của EF
=>AE=FB
CH=DH=7cm
=>OH=24cm
=>CE+DF=48cm
S CEFD=1/2*48*14=7*48=336cm2
Cho nửa đường tròn (O) đường kính AB, dây CD không cắt AB. Các đường vuông góc với CD tại C và D cắt AB tại E và F
a) Chứng minh rằng E và F đối xứng với nhau qua O
Tính \(S_{CDFE}\)biết AB=50cm; CD=14cm
Cho nửa đường tròn tâm O đường kính AB dây CD. Các đường vuông góc với dây CD tại C và tại D cắt AB theo thứ tự ở E và F. Tính diện tích tứ giác CDEF
a) Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường vuông góc với CD tại C và D tương ứng cắt AB ở M và N. Chứng minh rằng AM = BN
b) Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, N sao cho AM = BN. Qua M và qua N kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở C và D. Chứng minh rằng MC và ND vuông góc với CD
1/ Cho đường tròn (O) đường kính AB và 1 điểm C trên đường tròn.Từ O kẻ 1 đường thảng song song với dây AC , đường thảng này cắt tiếp tuyến tại B của đường tròn ở điển C A) CM: OD là phân giác của góc BOC b) CN: CD là tiếp tuyến của đường tròn
2/ Cho đường tròn (O;R), H là điểm bên trong đường tròn (H không trùng với O). Vẽ đưởng kính AB đi qua H (HB < HA). Vẽ dây CD vuông góc với AB tại H. CMR:
a) Góc BCA = 90 độ b) CH . HD = HB . HA c) Biết OH = R/2. Tính diện tích tam giác ACD theo R
3/ Cho tam giác MAB, vẽ đường tròn (O) đường kính AB cắt MA ở C, cắt MB ở D. Kẻ AP vuông góc CD , BQ cuông góc CD. Gọi H là giao điểm AD và BC. CM:
a) CP = DQ b) PD . DQ = PA . BQ và QC . CP = PD . QD c) MH vuông góc AB\
4/ Cho đường tròn (O;5cm) đường kính AB, gọi E là 1 điểm trên AB sao cho BE = 2cm.Qua trung điểm kH của đoạn AE vẽ dây cung CD vuông góc AB.
a) Tứ giác ACED là hình gì? Vì sao? b)Gọi I là giao điểm của DE với BC. CMR:I thuộc đường tròn (O') đường kính EB
c) CM HI là tiếp điểm của đường tròn (O') d) Tính độ dài đoạn HI
5/ Cho đường tròn (0) đường kính AB = 2R. Gọi I là trung điểm của AO, qua I kẻ dây CD vuông góc với OA.
a) Tứ giác ACOD là hình gì? tại sao?
b) CM tam giác BCD đều
c) Tính chu vi và diện tích tam giác BCD theo R
6/ Cho tam giác ABC vuông tại A có đường cao AH. Biết AB = 9cm; BC = 15cm
a) Tính độ dài các cạnh AC, AH, BH, HC
b) Vẽ đường tròn tâm B, bán kính BA. Tia AH cắt (B) tại D. CM: CD là tiếp tuyến của (B;BA)
c) Vẽ đường kính DE. CM: EA // BC
d) Qua E vẽ tiếp tuyến d với (B). Tia CA cắt d tại F, EA cắt BF tại G. CM: CF = CD + EF và tứ giác AHBG là hình chữ nhật
7/ Cho đường tròn (O) đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. gọi E là giao điểm của AC và BM.
a) CMR: NE vuông góc AB
b) Gọi F là điểm đối xứng với E qua M. CMR: FA là tiếp tuyến của đường tròn (O)
c) CM: FN là tiếp tuyến của đường tròn (B;BA)
8/ Cho nửa đường tròn (O), đường kính AB.Từ một điểm M trên nửa đường tròn ta vẽ tiếp tuyến xy. Từ A ta vẽ AD vuông góc với xy tại D
a) CM: AD // OM
b) Kẻ BC vuông góc với xy tại C. CMR: MC = MD
Cho đường tròn tâm O đường kính AB, dây cung CD vuông góc với AB tại H với H nằm giữa A và O. Trên tia đối của DC lấy điểm M. Đường thẳng MB cắt đường tròn tâm O tại F, FA cắt CD tại I
a. Chứng minh tứ giác BHÌ nội tiếp đưọc trong đường tròn
b. Chứng minh FA là phân giác của CFD
c. Tiếp tuyến của đường tròn (O) tại F cắt DM tại E. Chứng minh EI=EM
bạn gì đó giúp mình giải bài toán này vs
Cho đường tròn tâm O đường kính AB, M là điểm chính giữa của một nửa đường tròn (O) với đường kính AB, C là điểm bất kỳ trên nửa còn lại, CM cắt AB tại D. Vẽ dây cung AE vuông góc với CM tại F (E nằm trên đường tròn).
Chứng minh rằng tứ giác ACEM là hình thang cân.Vẽ CH vuông góc với AB (H nằm trên đoạn AB). Chứng minh rằng CM là phân giác góc HCO.Chứng minh rằng \(CD\le\frac{1}{2}AE\).1) Vì ^AEB chắn nửa đường tròn (O) nên EA vuông góc EB. Do đó BE // CM.
Suy ra tứ giác BECM là hình thang cân (Vì 4 điểm B,C,M,E cùng thuộc (O))
Kết hợp với M là điểm chính giữa cung AB suy ra CE = BM = AM hay (CE = (AM
Vậy thì tứ giác ACEM là hình thang cân (đpcm).
2) Đường tròn (O) có M là điểm chính giữa cung AB, suy ra MO vuông góc AB
Từ đó MO // CH suy ra ^HCM = ^OMC = ^OCM. Vậy CM là phân giác của ^HCO (đpcm).
3) Kẻ đường kính MG của đường tròn (O). Dễ thấy ^DOG = ^DCG (= 900)
Suy ra 4 điểm C,D,O,G cùng thuộc đường tròn đường kính DG
Mặt khác AB là trung trực của MG, D thuộc AB nên DG = DM
Theo mối quan hệ giữa đường kính và dây ta có:
\(CD\le DG=DM\Leftrightarrow2CD\le DM+CD=CM\Leftrightarrow CD\le\frac{1}{2}CM\)
Lại có tứ giác ACEM là hình thang cân, do vậy \(CD\le\frac{1}{2}CM=\frac{1}{2}AE\)(đpcm).
Dấu "=" xảy ra khi và chỉ khi C là điểm chính giữa cung AB không chứa M của (O).
Cho nửa đường tròn đường kính AB và một dây CD. Qua C vẽ đường thẳng vuông góc với CD, cắt AB tại I. Các tiếp tuyến tại A và B của nửa đường tròn cắt đường thẳng CD theo thứ tự tại E và F. Chứng minh rằng: Các tứ giác AECI và BFCI nội tiếp được
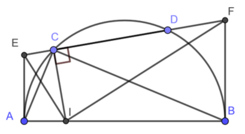
Vì AE, BF là các tiếp tuyến của nửa đường tròn nên

Cho (O:R) đường kính AB. Điểm H thuộc OB ( H không trùng O và B). Dây CD vuông góc với AB tại H, đường thẳng d tiếp xúc với đường tròn tại A. CO,DO cắt đường thằng d lần lượt tại M,N. CM và DN cắt đường tròn (O) lần lượt tại E,F.
a) Chứng minh tứ giác MNEF nội tiếp
b) chứng minh ME.MC=NF.ND
c)Tìm bị trí của H để tứ giác AEOF là hình thoi
d) Lấy K đối xứng cới C qua A. Gọi G là trọng tâm của tam giác KAB. Chứng minh rằng khi H chuyển động trên OB thì G thuộc 1 đường tròn cố định.