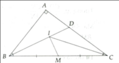
Cho tam giác ABC vuông tại A ,có phân giác BD, biết AB = 9 cm, BC = 15 cm .Tính AC, DC, DA?

Những câu hỏi liên quan
cho tam giác ABC Vuông tại A ( AB < AC)
a) Cho biết AB = 9cm , AC =12 cm . Tính BC
b) BD là Phân giác của góc B ( D thuộc AC ) . Vẽ DE vuông góc BC tại e. Chứng minh tam giác ABD = tam giác EDB
c) Chứng minh rằng DA <DC
a, Áp dụng Đ. L. Py-ta-go vào tg ABC vuông tại A, có:
BC2=AB2+AC2
=>BC2=92+122=81+144=225.
=>BC=15(cm)
b, Xét tg ABD và tg EBD, có:
góc ABD= góc DBE(tia phân giác)
BD chung.
góc A= góc E(=90o)
=>tg ABD= tg EBD(ch-gn)
Đúng 0
Bình luận (1)
Cho tam giác abc vuông tại a có ab 6 cm, bc 10 cm, bd là phân giác góc widehat{ABC} a)Tính da và dc b) Qua ac vẽ đường thẳng vuông góc với bd tại m cắt ab tại e. Chứng minh dfrac{em}{eb} dfrac{ea}{ec}
Đọc tiếp
Cho tam giác abc vuông tại a có ab= 6 cm, bc= 10 cm, bd là phân giác góc \(\widehat{ABC}\) a)Tính da và dc
b) Qua ac vẽ đường thẳng vuông góc với bd tại m cắt ab tại e. Chứng minh \(\dfrac{em}{eb}\) = \(\dfrac{ea}{ec}\)
Cho tam giác ABC vuông tại A ( AB < AC), BD là đường phân giác của góc B (D thuộc AC). Vẽ DE vuông góc BC tại E. a) Cho biết AB = 3 cm AC = 4 cm .Tính BC b) Chứng minh BD là đường trung trực của AE c) Chứng minh rằng DA < DC d) Vẽ CF vuông góc với BD tại F. Chứng minh rằng các đường thẳng AB, DE, CF đồng quy.
a, Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+AC^2\) (định lí Py - ta - go)
=> \(BC^2=3^2+4^2\)
=> \(BC^2=25\)
=> BC = 5 (cm)
b, Xét Δ ABD và Δ EBD, có :
\(\widehat{ABD}=\widehat{EBD}\) (BD là tia phân giác \(\widehat{ABE}\))
\(\widehat{BAD}=\widehat{BED}=90^o\)
BD là cạnh chung
=> Δ ABD = Δ EBD (g.c.g)
=> AB = AE
Xét Δ ABE, có :
AB = AE (cmt)
=> Δ ABE cân tại E
Ta có :
Δ ABE cân tại E
BD là tia phân giác của \(\widehat{ABE}\))
=> BD là đường trung trực của AE
Đúng 2
Bình luận (0)
c, Ta có : Δ ABD = Δ EBD (cmt)
=> AD = ED
Trong Δ CED, cạnh huyền DC là cạnh lớn nhất
=> ED < DC
Mà AD = ED (cmt)
=> AD < DC
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A . Có AB bằng 6 cm. AC bằng 8 cm. a tính độ dài cạnh BC và chu vi tam giác ABC . Đường phân giác của góc B cắt AC tại D .Vẽ DH vuông góc BC . [ H thuộc BC ]. CM tam giác ABD = tam giác HBD c CM DA < DC . có vẽ hình nha mọi người
a: BC=10cm
C=AB+BC+AC=6+8+10=24(cm)
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
c: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC
Đúng 2
Bình luận (0)
tam giác ABC vuông tại a có ab =3 ac =4 vẽ phân giác bd (d thuộc ac) từ d vẽ de vg góc bc (e thuộc bc) cm abd =ebd b,cm dc>da
Cho tam giác ABC vuông tại A (AB < AC), BD là đường phân giác. Vẽ DE ⊥ BC tại E
a) Cho biết AB=9 cm, AC = 12cm, Tính BCb
b) Chứng minh tam giác DAE cân
c) Chứng minh rằng DA < DC
d) Vẽ CF vuông góc với BD tại F. Chứng minh rằng các đường thẳng AB, DE, CF đồng quy
a, xét tam giác abc vuông tại a có
ab^2 + ac^2= bc^2
9^2+12^2=bc^2
144=bc^2
BC=12cm
b,có gì mái mình giải tiếp giờ đi học rồi
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB = 6 cm, AC = 8cm. Gọi BD là đường phân giác của tam giác ABC. a)Tính các độ dài DA, DC. b) Tia phân giác của góc C cắt BD tại I. Gọi M là trung điểm của BC. Chứng minh BIM = 90°.
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=36+64=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{DA}{AB}=\dfrac{DC}{BC}\)
=>\(\dfrac{DA}{6}=\dfrac{DC}{10}\)
=>\(\dfrac{DA}{3}=\dfrac{DC}{5}\)
mà DA+DC=AC=8cm(D nằm giữa A và C)
nên \(\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{8}{8}=1\)
=>\(DA=3\cdot1=3cm;DC=5\cdot1=5cm\)
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}=5\left(cm\right)\)
mà DC=5cm
nên CM=CD
Xét ΔCDI và ΔCMI có
CD=CM
\(\widehat{DCI}=\widehat{MCI}\)
CI chung
Do đó: ΔCDI=ΔCMI
=>\(\widehat{CID}=\widehat{CIM}\) và \(\widehat{IMC}=\widehat{IDC}\)(3)
Ta có: \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}\)(góc IDC là góc ngoài tại đỉnh D của ΔABD)
nên \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}=90^0+\widehat{ABD}\)(2)
Xét ΔBIM có \(\widehat{IMC}\) là góc ngoài tại đỉnh M
nên \(\widehat{IMC}=\widehat{MIB}+\widehat{MBI}\left(1\right)\)
Từ (1),(2),(3) suy ra \(\widehat{MIB}+\widehat{MBI}=90^0+\widehat{ABD}\)
mà \(\widehat{MBI}=\widehat{ABD}\)
nên \(\widehat{MIB}=90^0\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, AB = 6cm, AC= 8 cm, đường phân giác BD.
a) Tính các độ dài DA, DC.
b) Tia phân giác của góc C cắt BD ở I. Gọi M là trung điểm của BC. Chứng minh B I M ^ = 90 0
cho tam giác ABC vuông tại A , đường cao AH ,đường phân giác BD , kẻ HE vuông góc với AB . biết AB =6 CM , BC=10CM.hỏi tính AC , AH,BD,DC,BE